Volume Benda Putar, Rumus, dan Contoh Soal

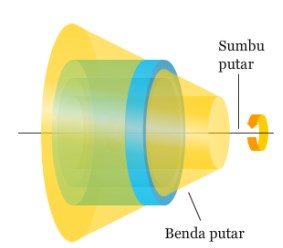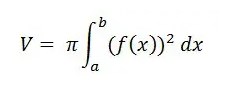
Baca juga: Cara Menghitung Volume Kerucut Yang Benar

2. Volume benda putar sumbu y yang dibatasi 1 kurva

Pada sebuah bangun benda putar yang memiliki sumbu y untuk mencari volume putarnya dapat mengubah persamaan grafik. Biasanya, grafik yang mulanya y dan menjadi fungsi x akan berubah dan menjadi terbalik dengan x menjadi fungsi y. Seperti pada rumus y = f(x) menjadi x = f(y). Misalnya, y = x² dan x = √y dapat diubah persamaannya dengan masuk pada rumus berikut.

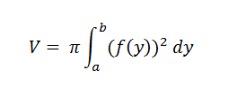
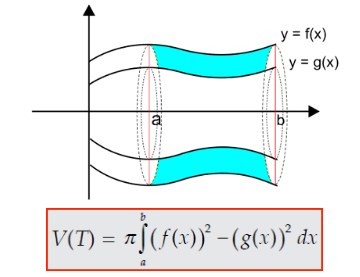
3. Volume benda putar yang dibatasi dua kurva jika diputar mengelilingi sumbu x

Volume benda putar dapat ditampilkan dengan sebuah luasan yang dibatasi oleh dua kurva yaitu f(x) dan g(x) yang ditunjukkan pada |f(x)| ≥ |g(x)| dengan interval [a,b] diputar mengelilingi sumbu x. Pada kasus ini, volume benda putar tersebut bisa dihitung menggunakan rumus sebagai berikut.

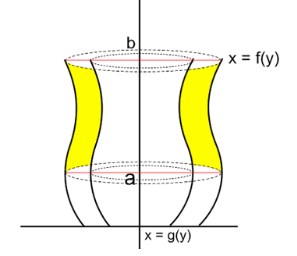
4. Volume benda putar yang dibatasi dua kurva jika diputar mengelilingi sumbu y

Volume benda putar dapat ditampilkan dengan sebuah luasan yang terbentuk dari dua buah kurva x = f(y) dan x = g(y) dan interval [a.b]. Putarannya dapat mengitari sumbu y maka volume yang dihasilkan bisa dicari menggunakan rumus berikut.

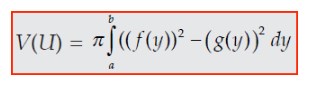
Baca juga: Rumus Volume Dan Luas Bola

Metode Menghitung Volume Benda Putar

Penghitungan volume benda putar dapat kita klasifikasikan menjadi dua jenis berdasarkan putaran sumbunya. Metode menghitungnya dapat kita pahami dengan menggunakan dua integral sebagai berikut.

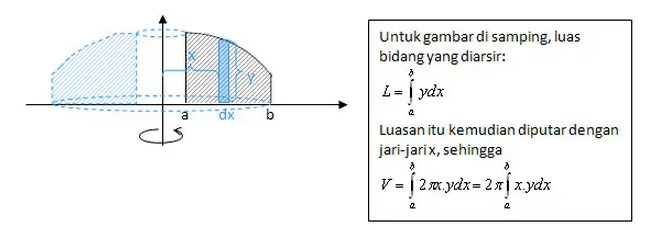
1. Metode cakram

Metode ini dapat diterapkan dengan rumus volume = luas alas x tinggi. Hal ini karena luas alas akan selalu berupa lingkaran pada sebuah cangkram dengan rumusnya πr² dan digunakan jika batang potongan tegak lurus dengan sumbu putar sebagai berikut.

2. Metode cincin silinder

Jika suatu luasan diputar pada sumbu tertentu akan terbentuk suatu benda putar dengan volume sebesar luasan itu dikali dengan keliling putaran. Hal ini karena keliling lingkaran adalah 2πr  dengan luas bidang yang diputar = A maka volume adalah 2πr × A, lalu dipakai jika batang potongan sejajar dengan sumbu putar seperti berikut.

Baca juga: Pengertian, Rumus Dan Contoh Soal Translasi

Contoh Soal

Setelah mempelajari pembahasan di atas mengenai volume benda putar hendaknya kalian pahami lebih lanjut dengan mempelajari beberapa pembahasan soal berikut ini.

1. Tentukan volume dari benda putar bila daerah yang dibatasai oleh fungsi f(x) = 4 -x2, sumbu x, dan sumbu y diputar 360º terhadap sumbu x.

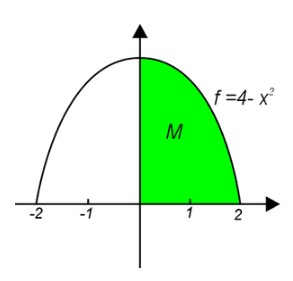
Pembahasan:

2. Hitunglah volume benda putar yang terjadi jika daereah yang dibatasi oleh kurva  y = √x , garis x = 2, garis y = 4, dan garis y = 3.

Pembahasan: