Fungsi Kuadrat Kelas 9 dan Contoh Soal – Ketika belajar ilmu matematika, terdapat salah satu materi mengenai fungsi kuadrat yang sering diterapkan di setiap macam-macam operasi matematika. Suatu fungsi dengan pangkat tertingginya adalah 2 (dua) yang bisa disajikan dalam bentuk pasangan berurutan, tabel, diagram panah dan grafik.
Fungsi dengan kuadrat menjadi pembahasan matematika yang dimaknai sebagai operasi perhitungan perpangkatan pada variabel tingkat 2. Dengan begitu, kuadrat merupakan nama lain dari angka yang dipangkatkan dengan nilai 2. persamaan kuadrat sendiri adalah persamaan yang terjadi dalam matematika dan memiliki variabel paling tinggi berderajat dua.
Baca Juga: Rumus Pemuaian Zat Padat dan Contoh Soal
Baca Juga: Gaya Pada Bidang Miring, Rumus dan Contoh Soal
Baca Juga: Reaksi Hidrokarbon, Subtitusi, Adisi dan Eliminasi
Pada pembahasan kali ini, kalian akan mempelajari mengenai materi fungsi kuadrat di kelas 9. Berikut pembahasannya.
Fungsi Kuadrat
Pengertian dari fungsi kuadrat dimaknai sebagai suatu fungsi yang berbentuk y = ax2 + bx + c , dengan a≠0,x,yϵR. Hal ini menjadikan a dan b adalah koefesien, x dan y adalah variabel dan c merupakan konstanta. Misalnya, pada bentuk fungsi f(x) = 2x2 – x + 3 memiliki bentuk umum sebuah fungsi yang berdasar dari f(x) = ax2 ± bx ± c, dengan a, b, dan c bilangan asli dan a≠ 0.
Grafik Fungsi Kuadrat
Hubungan nilai koefesien dan konstanta y = ax2 + bx + c memiliki penerapan terhadap bentuk grafik fungsi kuadrat. Nilai a pada fungsi y = ax2 + bx + c akan mempengaruhi bentuk grafiknya. Jika a positif maka grafiknya akan terbuka ke atas. Sebaliknya jika a negatif menjadikan grafiknya akan terbuka ke bawah. Jika nilai a semakin besar menjadikan grafiknya akan semakin kurus.
Nilai b pada grafik y = ax2 + bx + c menunjukan dimana koordinat titik puncak dan sumbu simetri berada. Jika a> 0 maka grafik y=ax2+bx+c akan memiliki titik puncak minimum. Jika a<0 menjadikan grafik y = ax2 + bx + c akan memiliki titik puncak minimum.
Nilai c pada grafik y = ax2 + bx + c menunjukkan titik perpotongan grafik fungsi kuadrat tersebut dengan sumbu-y. yakni koordinat (0,c)

Dalam menggambar grafik fungsi kuadrat, perhatikan langkah-langkah berikut ini.
- Langkah 1 Menentukan bentuk parabola (terbuka keatas atau kebawah)
- Langkah 2 Menentukan titik potong dengan sumbu-x (dimana y=0)
- Langkah 3 Menentukan titik potong sumbu-y (dimana x=0)
- Langkah 4 Menentukan sumbu simetri dan nilai optimum dari grafik fungsi
- Langkah 5 Mensketsa grafik sesuai dengan hasil dari langkah 1-4
Menentukan Akar Persamaan Kuadrat
Untuk menentukan akar persamaan kuadrat ada beberapa cara yang bisa kita gunakan seperti
1. Memfaktorkan
persamaan kuadrat x2+bx+c = 0 bisa kita faktorkan menjadi (x+p)(x+q)=0 dimana p+q=b dan p.q=c
2. Melengkapkan kuadrat sempurna persamaan kuadrat ax2+bx+c = 0 juga bisa kita cari akarnya dengan menggunakan cara melengkapkan kuadrat sempurna.
ax2+bx+c = 0
ax2+bx=-c
ax2+bx+(1/2 b)2=-c + (1/2 b)2
3. Rumus abc
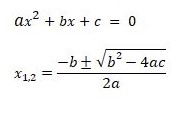
Jenis-jenis akar
Jenis akar persmaan kuadrat juga bisa kita tentukan dengan menggunakan nilai Determinannya. dimana

1. Jika D>0, maka persamaan kuadrat memiliki 2 buah akar yang berbeda, (artinya grafiknya memotong sumbu-x di 2 titik yang berbeda)
2. Jika D=0, maka persamaan kuadrat memiliki 2 buah akar kembar (artinya grafiknya hanya menyinggung sumbu-x di sumbu x)
3.Jika D<0, maka persamaan kuadrat tidak memiliki akar riil (artinya grafik tidak menyinggung maupun memtong sumbu-x)
Kesimpulan
- Menentukan titik potong
Memotong sumbu x jika y =0, maka titik potongnya (x1,0) atau (x2, 0)