Rumus Volume Dan Luas Bola

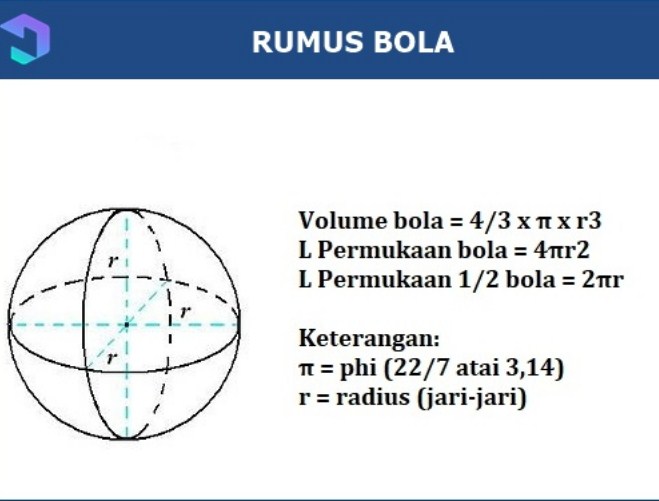
Rumus Volume Dan Luas Bola – Bola merupakan salah satu jenis bangun ruang yang wajib di pelajari. Materi mengenai bangun ruang bola sebenarnya sudah dibahas sejak kita masih duduk di bangku sekolah. Namun sayangnya masih banyak yang belum paham mengenai bangun ruang yang satu ini.

Nah, pada kesempatan kali ini kami akan membahas mengenai bangun ruang bola secara lengkap dan jelas mulai dari pengertian, sifat-sifat, serta rumus volume dan luasnya. Kami juga akan memberikan contoh soalnya sehingga bisa memudahkan Anda untuk memahami materi matematika yang akan kami sampaikan ini.  Mari langsung saja kita simak pembahasan selengkanya berikut ini.

Mengenal Bola Lebih Detail

Bola merupakan salah satu jenis bangun ruang sisi lengkung yang telah dibatasi oleh sebuah bidang lengkung. Bangun ruang bola ini dihasilkan dari bangun setengah lingkaran yang telah diputar hingga mencapai satu putaran penuh atau 360 derajat pada bagian garis tengahnya.

Dalam KKBI atau kamus besar bahasa Indonesia, arti dari bola adalah sebuah barang yang memiliki bentuk menyerupai bulat-bulatan. Berikut ini adalah contoh dari gambar bangun ruang bola.

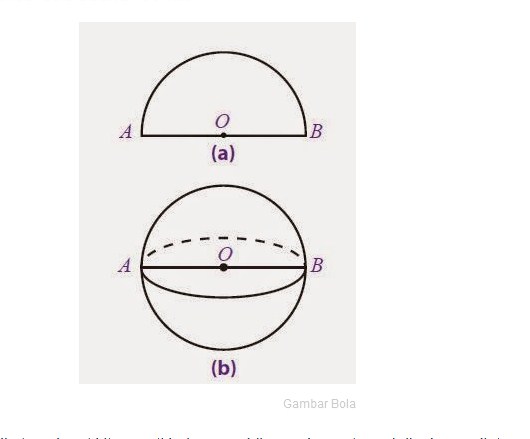
Dilihat dari gambar bangun ruang bola diatas, bisa kita amati jika gambar setengah lingkaran diatas apabila diputar hingga satu putaran penuh atau mencapai 360 derajat, pada bagian garis AB maka akan didapatkan sebuah bangun ruang bulat seperti pada gambar yang (b). Nah inilah yang disebut dengan bola.

Pengertian Permukaan Bola

Permukaan bola merupakan suatu luasan bidang yang membentuk permukaan sebuah bola atau yang biasa disebut dengan kulit bola atau selimut bola. Himpunan pada titik-titik yang memiliki jarak sama terhadap sebuah titik disebut dengan titik pusat, bisa diartikan juga sebagai sisi lengkung yang telah dibatasi oleh sebuah bidang lengkung.

Baca Juga:  Rumus Volume Bangun Ruang

Sifat-Sifat pada Bangun Ruang Bola

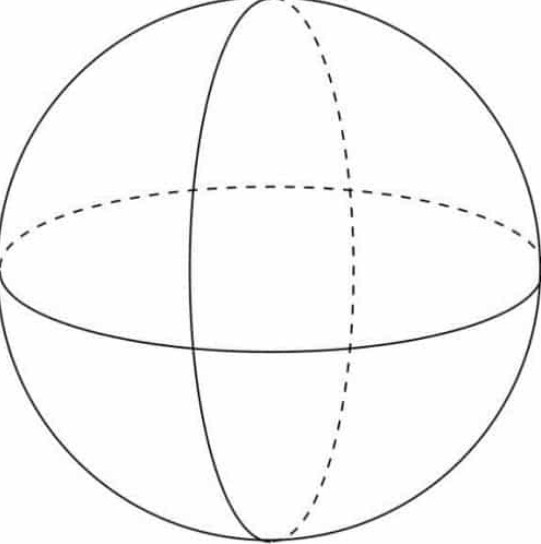
Bangun ruang bola memiliki beberapa sifat tertentu yang tidak dimiliki oleh bangun ruang lainnya. Adapun sifat-sifat pada bangun ruang bola adalah sebagai berikut ini:

• Bangun ruang bola mempunyai sisi lengkung.
• Bola tidak mempunyai titik sudut dan juga rusuk.
• Bola hanya mempunyai satu sisi dan satu titik pusat.
• Sisi bangun ruang bola biasa disebut dengan dinding bola.
• Jarak dinding ke bagian titik pusat bola disebut dengan jari-jari.
• Jarak dinding ke dinding dan melalui titik pusat disebut dengan diameter.

Luas dan volume Bola

• Luas bola :

L = 4 x luas lingkaran
= 4 x π r2
= 4 π r2

• Volume bola :

V = 4 x volume kerucut
= 4 x 1/3 π r2 t
karena pada bola, t = r maka
= 4 x 1/3 π r2 r
= 4 x 1/3π r3
= 4/3 π r3