3. Tentukan volume benda putar terbentuk dari daerah yang dibatasi oleh kurva y = x2dan y = –x2+ 6x dan diputar terhadap sumbu x.
Pembahasan:
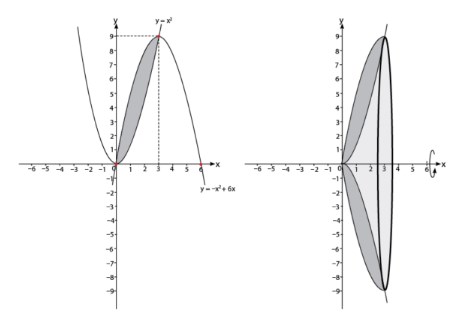
Dari sketsa gambar di atas dapat diperoleh bahwa perpotongan kedua kurva terdapat pada (0, 0) dan (3, 9). Volume dibentuk dengan memutar luas yang dibentuk kurva terhadap sumbu-x. Sehingga, batas integral yang digunakan berada pada titik-titik sumbu-x yaitu 0 dan 3. Jadi, batas integral dalam perhitungan volume adalah 0 sampai 3.
Penghitungan volume daerah yang dibatasi kurva y = x2 dan y = –x2 + 6x dan diputar terhadap sumbu x sebagai berikut.

4. Tentukan volume benda putar yang dibatasi kurva y = x, sumbu x, dan garis x = 3 yang diputar mengelilingi sumbu x sejauh 360 derajat.
Pembahasan:
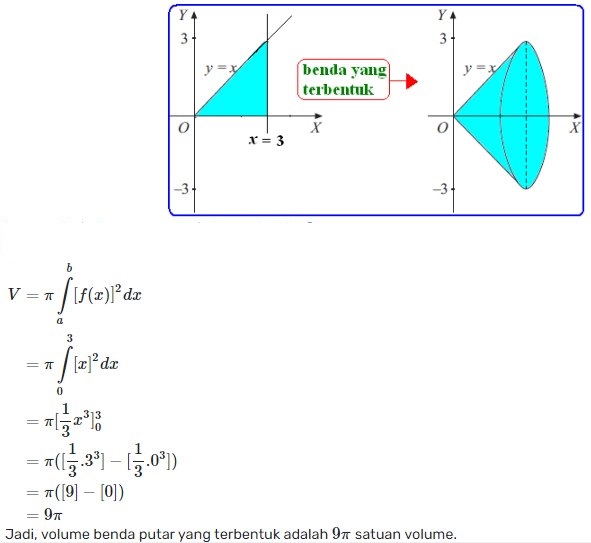
5. Tentukan volume benda putar dengan dibatasi sumbu Y berdasarkan kurva y = x2, garis y = 2, dan garis y = 5 mengelilingi sumbu Y.
Pembahasan: