Pengertian, Rumus Dan Contoh Soal Translasi

Rumus Dan Contoh Soal Translasi – Dalam materi matematika ilmu geometri mempunyai cakupan yang sangat luas. Selain mempelajari mengenai luas bangun datar, volume bangun ruang beserta sifat-sifatnya, kita juga dihadapkan dengan berbagai materi dan rumus lainnya. Salah satunya adalah transformasi geometri.

Tentu kalian sudah tahu bahwa transformasi berarti berubah bentuk. Dalam geometri transformasi adalah perubahan posisi atau perpindahan dari suatu posisi awal ke posisi lainnya. Transformasi dalam geometri terbagi menjadi beberapa macam, salah satunya adalah translasi.

Pada artikel ini kita bahas lebih lanjut mengenai translasi, berikut jenis-jenis transformasi geometri lainnya. Sehingga kita bisa mencermati apa saja perbedaan dari masing-masing jenis transformasi. Langsung saja kita simak pembahasan berikut.

Baca juga: Rumus Dan Contoh Soal Hubungan Antar Sudut

Jenis Transformasi Geometri

Jenis transformasi geometri dapat dibagi menjadi empat macam. Yakni translasi, rotasi, refleksi, dan dilatasi. Keempatnya mempunyai perbedaan yang begitu mencolok sehingga harus kita pahami sehingga tidak sampai tertukar. Kita awali dari translasi yang menjadi pembahasan inti.

Translasi

Pertama-tama kita bahas translasi atau pergeseran. Sesuai dengan namanya, translasi adalah jenis transformasi geometri dimana terjadi pergeseran titik di sepanjang garis yang lurus dengan arah dan jarak. Proses translasi ini hanya akan memindahkan titik saja.

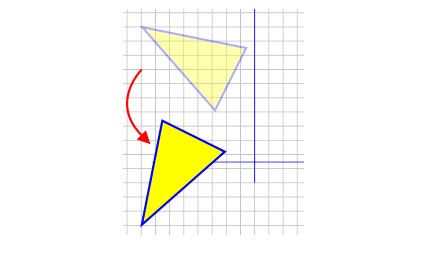
Ada trik mudah untuk menentukan hasil objek yang mengalami translasi. Yakni dengan cara menambahkan absis dan ordinat pada jarak tertentu sesuai dengan rumus. Lihat contoh di bawah ini.

Dari gambar contoh di atas kita bisa lihat bahwa bangun datar segitiga tersebut hanya mengalami perubahan posisi saja. Sedangkan ukuran, hingga titik-titik sudutnya tetap saja.

Rumus Translasi

(x’, y’) = (a, b) + (x, y)

Keterangan:

• (x’, y’) : titik bayangan
• (a, b) : vektor translasi
• (x, y) : titik asal

Refleksi

Selain translasi, jenis transformasi geometri lainnya adalah refleksi atau pencerminan. Refleksi merupakan jenis transformasi yang memindahkan titik pada bidang datar dengan memakai sifat seperti halnya pada bayangan cermin datar. Sementara hasil pencerminan tersebut nantinya tergantung dari jenis sumbu yang menjadi cermin titik tersebut. Simak gambar contoh berikut.

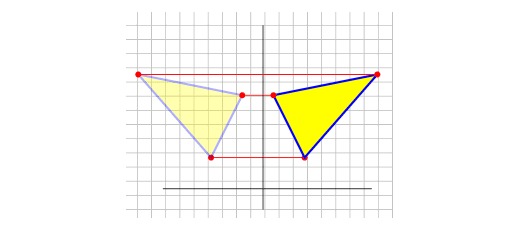
Berdasarkan gambar di atas, garis dan titik-titik merah terlihat berpindah posisi. Jika diperhatikan lebih rinci penampakan gambar tersebut sama halnya dengan sebuah cermin yang memantulkan bayangan dari objek yang ada di depannya.

Rumus Refleksi

• Pencerminan sumbu -x : (x, y) → (x, -y)
• Pencerminan sumbu -y : (x, y) → (-x, y)
• Pencerminan garis y = x : (x, y) → (y, x)
• Pencerminan garis y = -x : (x, y) → (-y, -x)
• Pencerminan garis y = h : (x, y) → (2h – x, y)
• Pencerminan garis y = k : (x, y) → (x, 2k – y)

Rotasi

Perputaran atau rotasi adalah transformasi geometri yang terdapat perubahan posisi pada objek dengan cara diputar dari sudut tertentu. Pada dasarnya rotasi merupakan perpindahan sebuah titik ke titik lainnya. Dalam rotasi prinsipnya adalah dengan memutar bangun datar terhadap sudut dan titik pusat tertentu yang jaraknya sama dengan setiap titik yang diputar. Di sisi lain rotasi tidak mengubah ukuran dari bangun datar yang diputar.