Penjelasan Komplemen Himpunan Dan Selisih Himpunan

Materi Komplemen Himpunan Dan Selisih Himpunan – Pada artikel kali ini kita kembali membahas materi mengenai himpunan. Khususnya penjelasan mengenai selisih himpunan dan komplemen himpunan. Seperti yang diketahui, materi tentang himpunan ini cukup luas, sehingga untuk memahaminya lebih baik kita perlu mempelajari materi-materi mengenai himpunan. Tak terkecuali komplemen dan selisih himpunan.

Sebagai pengingat, himpunan merupakan sekumpulan objek dan benda yang memiliki sifat yang dapat didefinisikan dengan jelas. Objek-objek atau benda yang terdapat dalam himpunan tersebut bisa kita sebut dengan istilah satu kesatuan. Dalam himpunan matematika juga terdapat yang namanya operasi himpunan. Operasi pada himpunan ini terbagi menjadi beberapa macam. Dua di antaranya adalah komplemen himpunan dan selisih himpunan.

Baik selisih himpunan maupun komplemen himpunan mempunyai karakteristik yang cukup berbeda. Cara menentukan selisih dan komplemen himpunan juga terdapat perbedaan. Oleh karenanya pada kesempatan ini kedua operasi himpunan itu yang kita bahas pada kesempatan ini. Kita awali dengan membahas komplemen terlebih dahulu. Silakan simak materi berikut.

Baca juga: Contoh Contoh Himpunan Dan Penjelasannya

Pengertian Komplemen Himpunan

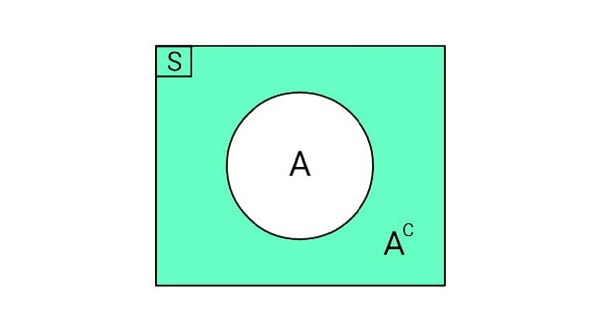
Secara singkat komplemen himpunan dapat diartikan sebagai suatu himpunan yang seluruh anggota dari himpunan semesta (S) yang bukan merupakan anggota dari himpunan A. Akan tetapi di sisi lain himpunan A juga berada di dalam himpunan semesta (S). komplemen dari himpunan A disebut sebagai A komplemen, serta dinyatakan dengan konotasi AC. S

Baca juga: Himpunan Irisan Dan Contoh Soal

Cara Menentukan Komplemen Himpunan

Dari penjelasan di atas kita sudah mengetahui apa itu komplemen himpunan. Yang menjadi pertanyaan selanjutnya adalah bagaimana cara menentukan komplemen himpunan. Ketika ingin menentukan komplemen himpunan, ada beberapa langkah yang perlu kita lakukan.  Berikut tahap menentukan komplemen himpunan:

• Langkah pertama : Tentukan semua hal yang diketahui dan yang dipertanyakan pada soal.
• Langkah kedua : Tuliskan semua anggota dari masing-masing himpunan, jika terdapat anggota himpunan yang sama, hilangkan anggota himpunan tersebut, sisanya tuliskan sebagai himpunan baru.
• Langkah ketiga : Tentukan komplemen himpunan.

Contoh 1

Sebuah himpunan semesta memiliki anggota H, J, B, M, L, G, O, R, dan P. Kemudian ada himpunan A yang beranggotakan J, L, G, R, dan P. Tentukan komplemen dari himpunan A.

Pembahasan :

Pertama, nyatakan himpunan S.

S = {H, J, B, M, L, G, O, R, P}

Kemudian deklarasikan himpunan A.

A = {J, L, G, R, P}

Perhatikan anggota dari himpunan S yang tidak termasuk anggota dari himpunan A. Himpunan inilah yang disebut sebagai A komplemen (AC). Jadi, dapat disimpulkan bahwa komplemen himpunan A adalah:

AC = {H, B, M, O}

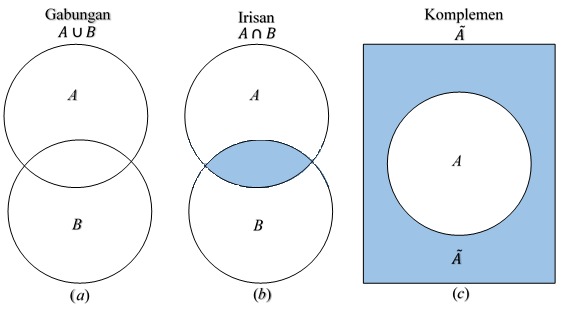
Contoh 2

Tentukan Komplemen B (Bc) dari :

S = {bilangan cacah}

B = {bilangan asli}

Penyelesaian :