Rumus Kesebangunan Bangun Datar

Rumus Kesebangunan Bangun Datar – Saat duduk di bangku sekolah menengah kita akan berhadapan dengan begitu banyak materi atau rumus dalam mata pelajaran matematika. Tentu saja kebanyakan materi yang diajarkan lebih rumit dibandingkan dengan saat di bangku sekolah dasar. Akan tetapi bukan berarti sulit untuk dikuasai. Asalkan kita bisa memahami materinya kita bisa menguasainya dengan baik.

Salah satu materi yang bisa membingungkan kita adalah kesebangunan bangun datar. Beberapa dari kalian pasti masih merasa asing dengan materi ini. Akan tetapi tidak perlu khawatir. Sebab pada kesempatan ini kami berikan materi seputar kesebangunan bangun datar untuk kalian. Sehingga kalian bisa membaca dan mempelajarinya, lengkap dengan contoh soalnya. Kita mulai dari apa itu kesebangunan.

Pengertian Kesebangunan

Perlu diketahui, kesebangunan merupakan salah satu materi yang diberikan dalam ilmu geometri. Kesebangunan ini berhubungan dengan membandingkan dua bangun datar. Kesebangunan adalah sebuah kondisi di mana dua bangun datar memiliki setiap sisi yang nilai perbandingannya sama. Tidak hanya itu, sudut dari dua bangun datar itu juga harus sama persis.

Baca juga: Sifat Sifat Bangun Datar Lengkap

Perbedaan Kesebangunan dan Kekongruenan

Jika dilihat dari definisi di atas mungkin kalian akan berpikir bahwa sebangun sama dengan kongruen. Akan tetapi sebenarnya keduanya berbeda. Sebuah bangun datar bisa disebut sebangun jika sisi-sisi dan sudut-sudut yang bersesuaian memiliki perbandingan yang sama besar.

Berbeda dengan kongruen, sebuah bangun datar dikatakan kongruen jika sisi-sisi yang bersesuaian sama panjang. Atau dengan kata lain dua bangun datar tersebut memiliki bentuk, ukuran dan sudut yang sama besarnya. Bisa disimpulkan bahwa seluruh bangun yang kongruen sudah pasti sebangun, namun bangun datar yang sebangun belum tentu kongruen.

Contoh dan Rumus Kesebangunan

Dari penjelasan di atas kita sudah memiliki gambaran seperti apa kesebangunan itu. Hanya saja mungkin sedikit sulit untuk membayangkannya. Maka dari itu lihat gambar di bawah ini.

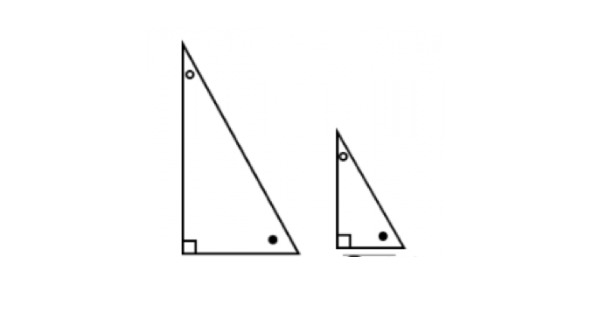
Di atas ada dua buah segitiga siku-siku yang sebangun. Ada tiga alasan mengapa demikian, yaitu:

1. Sudut-sudut yang bersesuaian sama besar (besaran tiap sudut kalo dibandingin dengan bangun lainnya sama besar)
2. Panjang sisi yang bersesuaian sama besar (panjang sisi kalo dibandingin memiliki nilai yang sama besar)
3. Perbandingan dua sisi yang bersesuaian kalo dibandingin memiliki panjang yang sama dan sudutnya sama.

Baca juga: Rumus Luas Dan Keliling Bangun Datar

Kesebangunan pada Persegi Panjang

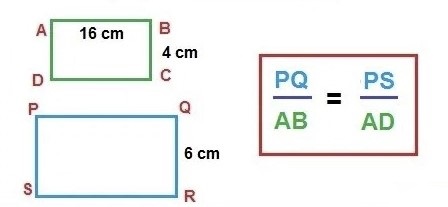
Kesebangunan pada Segitiga

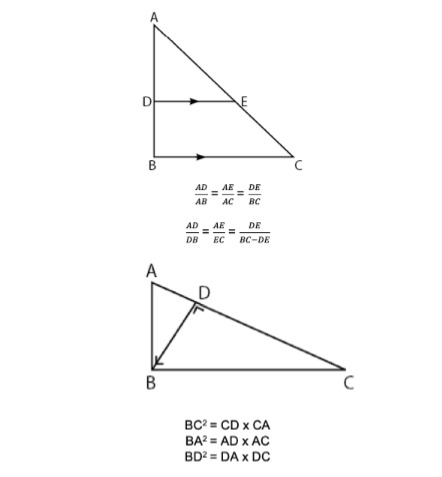
Kesebangunan pada Trapesium

Baca juga: Rumus Hubungan Antar Sudut

Contoh Soal

Di atas kita sudah membahas mengenai definisi kesebangunan, bedanya dengan kongruen, hingga contoh dan rumusnya. Tentu saja itu semua tidak cukup jika konteksnya adalah materi matematika. Tetap perlu ada contoh soal sehingga kita lebih paham dengan materi yang kita pelajari. Berikut beberapa contoh soal yang bisa kalian simak dan pahami.

Soal 1

Ada dua bangun segitiga ABE dan ACD yang jika kita lihat dari prinsip kesebangunan maka EB/DC = AB/AC. Panjang AB adalah 4 cm sedangkan panjang AC adalah 14 cm sedangkan tinggi EB adalah 150 cm. Cari dan hitung tinggi dari sisi DC!

Jawab:

Maka tinggi CD bisa ditemukan dengan menggunakan cara berikut: 

AC/AB = CD/BE 

14/4 = CD/1150 

CD = (150 x 14) : 4 

CD= 2100/4 

CD = 525 cm 

Jadi tinggi sisi CD pada segitiga ACD adalah 525 cm. +

Soal 2

Jika ada dua bangun persegi panjang ABCD dan PQRS, dengan panjang dan lebar bangun ABCD 16 cm x 4 cm. Jika lebar bangun PQRS adalah 6 cm, berapakah panjang sisi PQ?

Jawab: