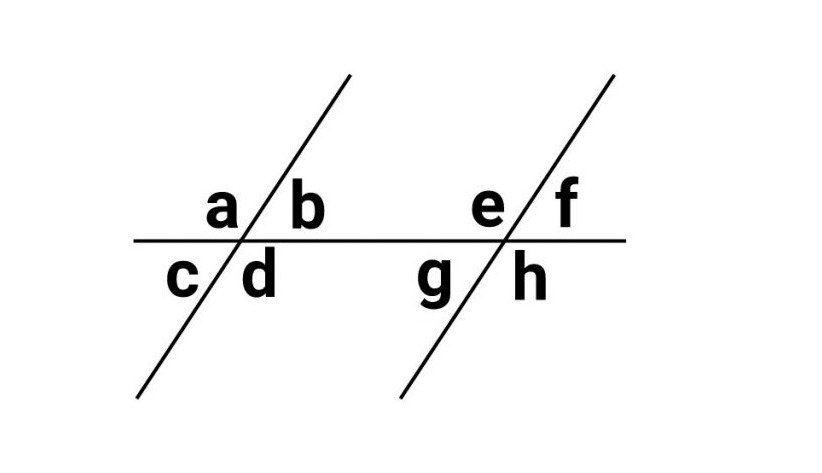
Rumus Hubungan Antar Sudut Dan Contoh Soal

Rumus Hubungan Antar Sudut Dan Contoh Soal – Pada artikel kali ini kita akan bahas materi tentang hubungan antar sudut. Seperti yang diketahui, bangun-bangun datar yang kita kenal selama ini umumnya mempunyai satu atau lebih sudut. Kecuali bangun datar lingkaran. Dan kita bisa mempelajari sudut-sudut tersebut, termasuk hubungan dan rumusnya.

Berikut penjelasan selengkapnya yang kita awali dari definisinya.

Definisi Sudut

Pertama-tama kita harus mengetahui apa itu sudut. Sudut adalah bagian pada suatu bangun datar atau ruang yang dibentuk oleh pertemuan antara dua sinar atau garis lurus. Sementara garis adalah susunan titik-titik yang saling bersebelahan dan berderet memanjang ke dua arah.

Sudut juga dapat diartikan sebagai daerah yang terbentuk dari sinar yang diputar pada pangkal sinar. Sudut ini dianotasikan dengan simbol “∠”.

Dalam matematika sudut bisa diartikan sebagai daerah yang terbentuk karena adanya dua garis sinar yang titik pangkalnya berhimpit atau bersekutu. Sedangkan dalam geometri sudut adalah besaran rotasi suatu ruas garis dari satu titik pangkal ke posisi lainnya. Dalam bangun dua dimensi yang beraturan, sudut didefinisikan sebagai ruang antara dua ruas garis lurus yang saling berpotongan.

Baca juga: Rumus Sudut Segitiga

Bagian pada Sudut

Sudut memiliki beberapa bagian yang bisa kita pelajari. Setidaknya ada tiga bagian dari sudut, antara lain:

1. Kaki sudut: adalah garis sinar yang membentuk sudut tersebut.
2. Titik sudut: adalah titik potong atau titik pangkal yang menjadi tempat berhimpitnya garis.
3. Daerah sudut: merupakan ruang atau daerah yang ada di antara dua kaki sudut.

Jenis Sudut

Selain mempunyai beberapa bagian, sudut juga terbagi menjadi beberapa macam dengan karakteristik atau ciri khas yang berbeda. Berikut beberapa jenis sudut tersebut:

1. Sudut siku-siku: merupakan sudut yang besarnya 90°.
2. Sudut lurus: sudut yang besarnya mencapai 180° dengan bentuk garis lurus.
3. Sudut lancip: sudut yang besarnya lebih dari 0° dan kurang dari 90°.
4. Sudut tumpul: merupakan kebalikan dari sudut lancip, yakni sudut yang besarnya lebih dari 90° dan kurang dari 180°.
5. Sudut refleks: merupakan sudut yang besarnya lebih dari 180° serta kurang dari 360°.

Selain sudut-sudut di atas, masih ada sudut-sudut lain yang bisa kita pelajari. Seperti gabungan dua sudut yang menghasilkan suatu hubungan. Dan inilah materi inti dari yang kita bahas pada pembahasan ini.

Hubungan Dua Sudut

Setelah membahas beberapa hal mengenai definisi sudut dan jenisnya, kini kita bahas mengenai hubungan dua sudut. Perlu diketahui bahwa pada hubungan dua sudut terdapat beberapa macam yang harus kita ketahui. Antara lain sudut yang saling berpelurus, berpenyiku, dan bertolak belakang. Silakan simak pembahasannya di bawah ini.

Sudut Saling Berpelurus (Bersuplemen)

Sudut ini juga dikenal sebagai sudut yang saling bersuplemen. Simak gambar berikut ini.

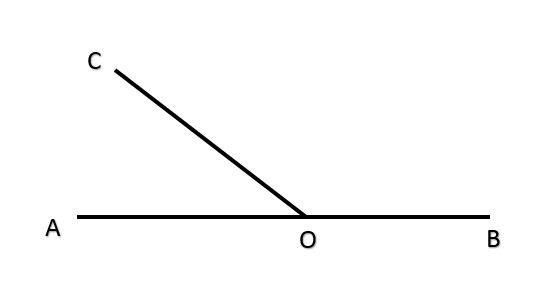
Dari contoh gambar di atas kita tahu bahwa dari titik A ke titik B membentuk ∠AOB yang besarnya 180°. Kemudian jika diperhatikan lagi pada titik O dibuat garis melalui C. Sehingga terbentuklah ∠AOC dan ∠BOC.

∠AOC adalah sudut berpelurus dari ∠BOC. Sehingga ketika ∠AOC + ∠BOC akan menghasilkan 180°. Dapat disimpulkan bahwa dua sudut disebut berpelurus atau bersuplemen jika saat ditambahkan menghasilkan 180°.

Sudut Saling Berpenyiku (Berkomplemen)

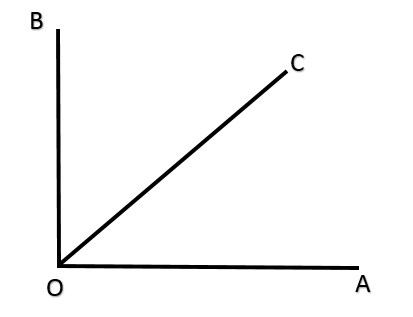
Sesuai dengan namanya, sudut berpenyiku adalah dua sudut yang jika dijumlahkan menghasilkan 90°. Dari contoh gambar di atas kita bisa lihat pada titik O dibuat garis melalui C. Sehingga terbentuk ∠AOC dan ∠BOC.

Pada kasus ini, jika kita menjumlahkan kedua sudut tersebut akan kita peroleh hasil 90°. Maka dari itu dua sudut dikatakan berpenyiku atau berkomplemen jika saat dijumlahkan akan menghasilkan 90°.

Sudut Saling Bertolak Belakang

Dari namanya tentu kita bisa langsung tahu apa arti dari hubungan dua sudut yang satu ini. Sudut yang saling bertolak belakang adalah sudut yang arah hadapnya saling berlawanan. Yang perlu dicatat besar sudut yang bertolak belakang ini sama. Simak gambar di bawah ini.

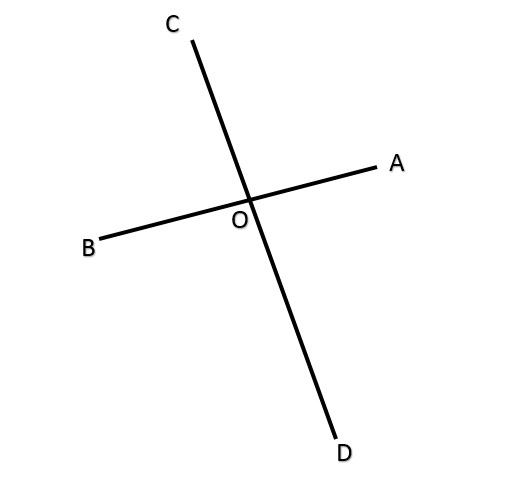
Dari gambar di atas terlihat garis AB dan CD merupakan garis lurus yang berpotongan di titik O. Sehingga terbentuk pasangan sudut hasil dari perpotongan tersebut. Yakni ∠AOC dan ∠BOD atau ∠BOC dan ∠AOD. Pasangan sudut-sudut tersebut yang bisa kita sebut sebagai sudut yang bertolak belakang.

∠AOC + ∠BOC = 180°

∠AOC = 180° – ∠BOC … (i)