Pertidaksamaan Linear Dua Variabel

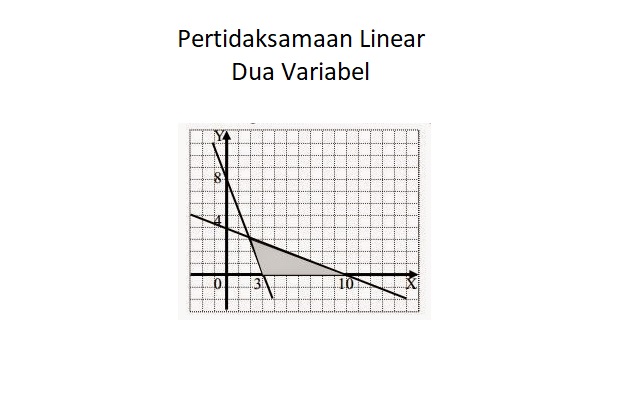
Langkah 3: mengarsir daerah yang bersesuaian dengan tanda pertidaksamaan

Daerah di bawah garis adalah tanda untuk kurang dari (<) dan daerah di atas garis adalah untuk tanda lebih dari (>). Daerah dari pertidaksamaan 4x + y < 20 dan x + y >= 10 adalah:

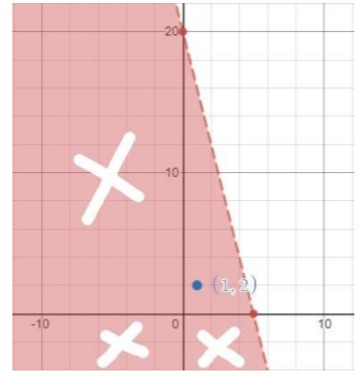
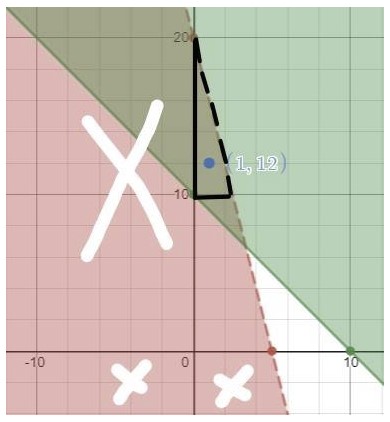
Perlu dicatat, jumlah apel dan mangga tidak akan bernilai negatif. Maka dari itu daerah yang diberi tanda silang bukan merupakan daerah penyelesaian. Dengan kata lain banyaknya keranjang mangga dan apel yang dapat dibawa 1 gerobak bisa kita lihat pada titik-titik yang berada di daerah penyelesaian.

Misalnya dari grafik di atas kita pilih titik x = 1 dan y = 12. Sehingga gerobak bisa membawa 1 keranjang apel dan 12 keranjang mangga dengan berat (4 x 1) + (1 x 12) = 4 + 12 = 16 kg. Dari hasil tersebut beratnya tetap di bawah 20 kg. Dengan total karung 13 (lebih dari ketentuan 10 karung)

Baca juga: Materi Persamaan Linear Dua Variabel

Contoh Soal

Soal 1

Himpunan penyelesaian dari |2x – 5| ≤ 9 adalah …

1. x ≤ -2 atau x ≥ 7
2. x ≤ 2 atau x ≥ 7
3. x ≤ 7
4. 2 ≤ x ≤ 7
5. -2 ≤ x ≤ 7

Jawab :

|2x – 5| ≤ 9

-9 ≤ 2x – 5 ≤ 9

-9 + 5 ≤ 2x – 5 + 5 ≤ 9 + 5

-4 ≤ 2x ≤ 14

-2 ≤ x ≤ 7

Jawaban E

Soal 2

Himpunan penyelesaian dari |4x + 1| > 9 adalah ….

1. x > 2
2. x < -5/2
3. x < -5/2 atau x > 2
4. -5/2 < x < 2
5. x > -5/2

Jawab :

|4x + 1| > 9

4x + 1 < -9 atau 4x + 1 > 9

4x < -10 atau 4x > 8

x < -5/2 atau x > 2

Jawaban C

Soal 3

Himpunan penyelesaian dari |2x – 5| ≤ 9 adalah …

1. x ≤ -2 atau x ≥ 7
2. x ≤ 2 atau x ≥ 7
3. x ≤ 7
4. 2 ≤ x ≤ 7
5. -2 ≤ x ≤ 7

Jawab :

|2x – 5| ≤ 9

-9 ≤ 2x – 5 ≤ 9

-9 + 5 ≤ 2x – 5 + 5 ≤ 9 + 5

-4 ≤ 2x ≤ 14

-2 ≤ x ≤ 7

Jawaban E

Baca juga: Materi Persamaan Linear Tiga Variabel

Soal Pertidaksamaan Linear Yang Pernah Keluar Di Ujian Nasional

Soal 1: UN 2020

Di dalam kandang terdapat kambing dan ayam sebanyak 13 ekor. Jika jumlah kaki hewan tersebut 32 2kor, maka jumlah kambing dan ayam masing-masing adalah….

A. 3 dan 10

B. 4 dan 9

C. 5 dan 8

D. 10 dan 3

Jawab:

Misalkan: