Persamaan Linear Dua Variabel – Pada kesempatan kali ini kami akan membahas mengenai materi sistem persamaan linear dua variabel. Selain SPLDV atau sistem persamaan linear dua variabel ini sebenarnya ada pula materi sistem persamaan satu variabel. Materi ini pada umumnya sudah dipelajari pada saat duduk di bangku SMP atau sederajat.
Lalu apa perbedaan antara sistem persamaan satu variabel dengan sisten persamaan liner dua variabel? Untuk sistem persamaan linear satu variabel persamaannya hanya memiliki satu variabel saja. Sementara itu untuk sistem persamaan linear dua variabel persamaannya sudah memiliki dua variabel. Untuk penjelasan lebih detail seperti rumus, cara mengerjakan dan contoh soal bisa dilanjutkan pembahasan selanjutnya.

Pengertian SPLDV atau sistem persamaan linear dua varibel adalah suatu persamaan yang memut dua variabel yang dimana untuk derajat atau pangkat pada setiap variabelnya sama dengan satu. Adapun bentuk umum dari persamaan linear dua variabel adalah sebagai berikut:
ax + by = c
Dari keterangan diatas x dan y adalah variabel.
Sistem Persamaan Linear Dua Variabel (SPLDV)
Sistem persamaan linear dua variabel atau yang biasa disebut dengan SPLDV adalah dua persamaan linear dua variabel yang memiliki hubungan diantara keduanya dan memiliki satu penyelesaian.
Berikut ini adalah bentuk umum dari sistem persamn linear dua variabel:
ax + by = c
px + qy = d
Ket:
- x dan y adalah variabel
- a, b, p, dan q adalah koefisien
- c dan r adalah konstanta
Sistem persamaan linear dua varibel pada umumnya digunakan untuk mengatasi masalah dalam kehidupan sehari-hari yang sekiranya memerlukan pemakaian ilmu matematika. Misalnya jika Anda ingin menentukan harga pada suatu barang, mencri keuntungan dalam jualan, sampai dengan menentukan ukuran sebuah benda.
Adapun langkah-langkah tertentu untuk menyelesaikan suatu masalah dengan menggunakan sistem persamaan linear dua variabel adalah sebagai berikut:
- Mengganti setiap besaran yang ada dalam masalah itu sendiri dengan menggunakan variabel (umumnya dinyatakan dengan simbol atau huruf).
- Membuat model matematika dari masalah itu sendiri. Model matematika ini selanjutnya dirumuskan dengan mengikuti bentuk umum SPLDV.
- Mencari solusi yang tepat dari permasalah tersebut, caranya adalah dengan menggunakan metode penyelesaian SPLDV.
Suku, Koefisien, Konstantan dan Variabel
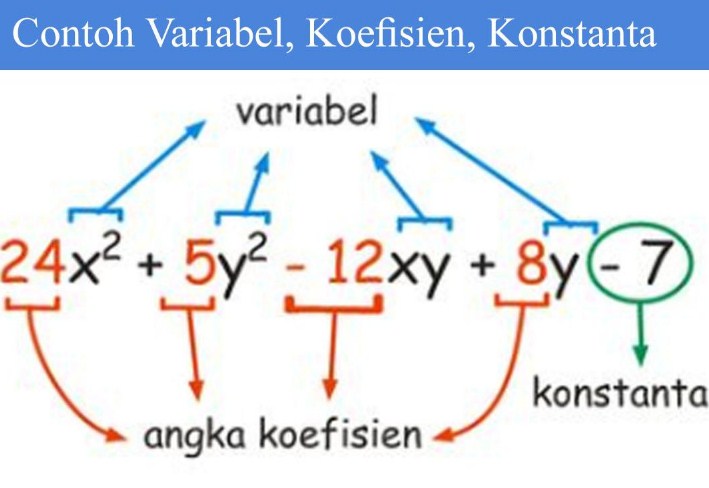
Suku adalah sebuah bagian dari bentuk aljabar yang terdiri atas variabel dan koefisien yang berupa konstanta bahwa masing-masing suku akan dipisahkan oleh suatu tanda operasi suatu penjumlahan.
Contoh:
5x-y + 8,
Pada suku diatas maka sukunya yaitu 5x-, -t dan 8
Variabel adalah sebuah dari suatu nilai atau angka yang biasanya dilambangkan oleh simbol atau huruf.