Persamaan Linear Satu Variabel

Persamaan Linear Satu Variabel – Pada artikel ini membawa materi persamaan linear satu variabel. Materi ini adalah materi lanjutan dari sistem persamaan yang ada pada mata pelajaran matematika. Yuk kita awali dari pengertiannya terlebih dahulu.

Apa itu Persamaan Linear Satu Variabel

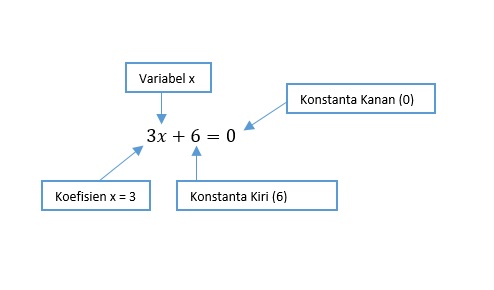
Perlu kalian ketahui bahwa persamaan linear satu variabel adalah kalimat terbuka yang mempunyai tanda hubung sama dengan (=). Tidak hanya itu, persamaan ini juga mempunyai satu variabel berpangkat 1.Bentuk umum dari persamaan linear satu variabel adalah ax + b = 0. Contohnya bisa kalian lihat di bawah ini:

1. x + 3 = 7
2. 3a + 4 = 1
3. r2– 6 = 10

Dalam materi ini kita perlu mengetahui beberapa elemen yang terdapat pada persamaan linear satu variabel. Antara lain pernyataan, variabel, konstanta, dan kalimat terbuka. Berikut definisi masing-masing elemen tersebut:

1. Kalimat terbuka: merupakan kalimat yang nilai kebenarannya belum bisa diketahui.
2. Variabel: juga biasa disebut peubah, yakni simbol atau lambang yang terdapat pada kalimat pembuka dan bisa diganti oleh sembarang anggota himpunan yang sudah ditentukan.
3. Konstanta: merupakan lambang yang dipakai untuk menyatakan suatu bilangan tertentu.
4. Himpunan penyelesaian: adalah himpunan seluruh pengganti dari variabel-variabel pada kalimat pembuka yang membuka kalimat tersebut menjadi benar.

Contoh dari himpunan penyelesaian adalah sebagai berikut:

1. x + 13 = 17
2. 7 – y = 12
3. 4z – 1 = 11

Penjelasan:

1. (x + 13 = 17) disebut kalimat terbuka, nilai x disebut variabel, sedangkan 13 dan 17 disebut dengan konstanta). Himpunan penyelesaiannya adalah x = 4
2. (7 – y = 12) disebut dengan kalimat terbuka, nilai y disebut dengan variabel, sedangkan 7 dan 12 disebut dengan konstanta. Himpunan penyelesaiannya adalah y = -5
3. (4z – 1 = 11) disebut dengan kalimat terbuka, nilai z disebut dengan variabel, sedangkan – 1 dan 11 disebut dengan konstanta. Himpunan penyelesaiannya adalah z = 3. 

Baca juga: Sistem Persamaan Linear Dua Variabel

Kesetaraan PLSV

Dua persamaan atau lebih dapat dinyatakan setara atau ekuivalen jika keduanya memiliki himpunan penyelesaian yang sama dan dinotasikan dengan simbol  “ ↔ “. Akan tetapi ada syarat tertentu yang perlu dipenuhi. Suatu persamaan bisa dinyatakan ke dalam suatu persamaan yang setara apabila dilakukan dengan cara berikut:

1. Menambah atau mengurangi kedua ruas dengan bilangan yang sama.
2. Mengalikan atau membagi kedua ruas dengan bilangan yang sama.

Baca juga: Sistem Persamaan Linear Tiga Variabel

Cara Menyelesaikan PLSV

Untuk menyelesaikan persamaan linear satu variabel kita harus memahami cara mengerjakannya. Ada tiga cara yang bisa kita gunakan, yakni dengan substitusi, dengan menambahkan atau mengurangi kedua ruas dengan bilangan yang sama, dan mengalikan atau membagi kedua ruas dengan bilangan yang sama.

Substitusi

Pertama kita bahas cara substitusi. Cara ini dilakukan dengan mengganti atau menyubstitusi variabel dengan suatu bilangan. Dengan begitu persamaannya bisa menjadi benar. Contohnya adalah sebagai berikut:

x + 2 = 5, dengan x adalah anggota bilangan asli.

• Untuk x = 1 maka 1 + 2 = 5 adalah kalimat yang salah.
• Untuk x = 2 maka 2 + 2 = 5 adalah kalimat yang salah.
• Untuk x = 3 maka 3 + 2 = 5 adalah kalimat yang benar.
• Untuk x = 4 maka 4 + 2 = 5 adalah kalimat yang salah.

Jadi, penyelesaian dari persamaan tersebut adalah x = 3.

Menambah atau Mengurangi

Cara kedua adalah menjumlahkan atau mengurangi persamaan dengan bilangan yang sama. Lebih jelasnya kalian lihat contoh berikut:

x – 4 = 13, dengan x anggota bilangan asli.

x – 4 + 4 = 13 + 4 (kedua ruas ditambah 4)

x = 17

Jadi, penyelesaian persamaan tersebut adalah x = 17.

Mengali atau Membagi

Selain menambahkan atau mengurangi, kita juga bisa mengalikan atau membagi persamaan dengan bilangan yang sama. Contohnya bisa kalian lihat di bawah:

1/2x = 28, dengan x anggota bilangan asli.

2 (1/2x) = 2 (28)

x = 56