Persamaan Linear Tiga Variabel

Persamaan Linear Tiga Variabel – Dalam sistem persamaan ada beberapa jenis yang bisa kita temui. Selain persamaan linear satu atau dua variabel, juga ada persamaan linear tiga variabel. Apa itu dan bagaimana cara menyelesaikannya? Untuk menjawab pertanyaan tersebut silakan pelajari materi berikut ini.

Apa itu Persamaan Linear Tiga Variabel

Sebagai pembuka kita harus berkenalan dengan persamaan linear tiga variabel. Dalam beberapa cabang ilmu, seperti ilmu arsitektur, kita perlu memanfaatkan perhitungan matematika supaya pekerjaan yang kita lakukan bisa lebih sempurna. Dan di sinilah sistem persamaan linear berperan.

Baca juga: Contoh Persamaan Linear Satu Variabel

Perhitungan pada sistem persamaan linear tidak hanya bertujuan untuk mengasah kemampuan kita dalam berpikir dan menyelesaikan suatu persoalan saja. Akan tetapi juga untuk menentukan koordinat titik potong. Dalam dunia arsitektur kita harus mengetahui koordinat yang tepat supaya bangunan yang kita dirikan sesuai dengan sketsa. Untuk itu digunakan rumus tersebut.

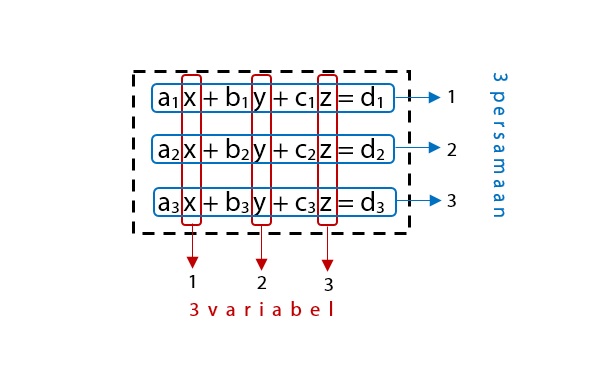
Sistem persamaan linear tiga variabel atau disingkat SPLTV adalah sebuah persamaan matematika yang terdiri dari tiga persamaan linear, dimana masing-masing persamaan tersebut memiliki tiga variabel. Sistem persamaan linear tiga variabel ini merupakan perluasan dari sistem persamaan linear dua variabel.

Sudah disinggung di atas bahwa sistem persamaan linear tiga variabel terdiri dari beberapa persamaan linear dengan tiga variabel. Bentuk umum persamaan ini adalah:

ax + by + cz = d

a, b, c, dan d adalah bilangan real. Meski begitu a, b, dan c tidak boleh bernilai nol (0) semua. Selain itu masih ada bentuk lain yang bisa kita jumpai, yaitu:

Cara mengerjakan persamaan ini cukup beragam. Dan akan kita bahas bersama pada artikel ini.

Baca juga: Contoh Persamaan Linear Dua Variabel

Ciri-ciri SPLTV

Sistem persamaan linear tiga variabel mempunyai beberapa ciri-ciri yang dapat kita amati, yakni:

1. Menggunakan relasi tanda sama dengan (=)
2. Memiliki tiga variabel
3. Ketiga variabel tersebut memiliki derajat satu (berpangkat satu)

Komponen SPLTV

Sistem persamaan linear tiga variabel terdiri dari beberapa komponen pembentuk. Berikut penjelasan singkat masing-masing komponen tersebut:

1. Variabel: merupakan notasi pengganti bilangan yang belum diketahui nilainya. Variabel juga sering disebut dengan istilah peubah. Biasanya variabel dinyatakan dalam huruf kecil.
2. Konstanta: merupakan suku dari bentuk aljabar yang berupa bilangan dan tidak memiliki variabel. Contohnya pada bentuk aljabar 3x + 5 yang merupakan konstanta adalah 5.
3. Koefisien: adalah faktor konstanta dari suatu suku pada bentuk aljabar. Misalnya pada bentuk aljabar 5x + 10, yang merupakan koefisien adalah 5.
4. Suku: adalah variabel dan koefisen atau konstanta pada suatu aljabar yang dipisahkan oleh operasi penjumlahan atau pengurangan.

Penyelesaian SPLTV

Dalam sistem persamaan linear tiga variabel terdapat tiga cara yang bisa kita pakai untuk menyelesaikannya. Yakni dengan eliminasi, substitusi, atau dengan gabungan. Lebih jelasnya berikut penjelasan masing-masing.

Eliminasi

Cara pertama adalah dengan eliminasi. Pada metode ini kita perlu menghilangkan salah satu variabel pada dua persamaan. Cara ini dilakukan terus sampai tersisa hanya satu variabel saja.

Pada dasarnya metode ini bisa diaplikasikan pada semua bentuk sistem persamaan linear tiga variabel. Hanya saja cara pengerjaannya terbilang panjang, sebab setiap langkah hanya bisa menghilangkan satu variabel saja. Di sisi lain kita perlu melakukan setidaknya tiga kali metode eliminasi untuk menentukan himpunan penyelesaian dari suatu persamaan linear tiga variabel.

Langkah menyelesaikan persamaan linear tiga variabel dengan metode eliminasi adalah sebagai berikut:

1. Amati ketiga persamaan pada SPLTV. Jika terdapat dua persamaan yang memiliki nilai koefisien sama pada variabel yang sama, kurangkan atau jumlahkan kedua persamaan tersebut agar variabel tersebut berkoefisien 0.
2. Jika tidak terdapat variabel dengan koefisien sama, kalikan kedua persamaan dengan bilangan yang membuat koefisien suatu variabel pada kedua persamaan tersebut menjadi sama. Kurangkan atau jumlahkan kedua persamaan agar variabel tersebut berkoefisien 0.
3. Ulangi langkah 2 untuk pasangan persamaan lain. Variabel yang dihilangkan pada langkah ini harus sama dengan variabel yang dihilangkan pada langkah 2.
4. Setelah diperoleh dua persamaan baru pada langkah sebelumnya, tentukan himpunan penyelesaian kedua persamaan menggunakan metode penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV).
5. Subtitusikan nilai dua variabel yang diperoleh pada langkah ke-4 pada salah satu persamaan SPLTV sehingga diperoleh nilai dari variabel ketiga.

Substitusi

Metode berikutnya adalah substitusi. Caranya adalah dengan mengganti atau melakukan substitusi nilai salah satu variabel pada satu persamaan ke persamaan lain. Cara ini dilakukan terus hingga kita mendapatkan semua nilai variabel dalam SPLTV. Cara ini bisa digunakan pada SPLTV yang memiliki persamaan dengan koefisien 0 atau 1. Langkah-langkah menyelesaikan SPLTV dengan metode ini adalah sebagai berikut:

1. Tentukan persamaan yang memiliki bentuk sederhana (memiliki koefisien 1 atau 0).
2. Nyatakan salah satu variabel dalam bentuk dua variabel lain.
3. Subtitusikan nilai variabel yang diperoleh pada langkah 2 ke persamaan lain pada SPLTV, sehingga diperoleh Sistem Persamaan Linear Dua Variabel (SPLDV).
4. Tentukan penyelesaian dari SPLDV yang diperoleh pada langkah 3.
5. Tentukan nilai semua variabel yang belum diketahui

Gabungan

Metode terakhir adalah gabungan. Caranya adalah dengan menggabungkan metode eliminasi dan substitusi. Pertama-tama kita gunakan metode eliminasi terlebih dahulu, lalu diikuti dengan metode substitusi. Atau juga bisa dibalik dengan melakukan substitusi terlebih dahulu.

Baca juga: Contoh Pertidaksamaan Linear Satu Variabel

Contoh Soal

Soal 1 (Dengan Metode Eliminasi)

2x + 3y – z = 20 … (1)

3x + 2y + z = 20 … (2)

X + 4y + 2z = 15 … (3)

SPLTV dapat ditentukan himpunan penyelesaiannya dengan mengeliminasi variabel z. Pertama, jumlahkan persamaan (1) dan (2) sehingga diperoleh:

2x + 3y – z = 20

3x + 2y + z = 20 +

5x + 5y       = 40

x + y           = 8 … (4)

Kemudian, kalikan 2 pada persamaan (2) dan kalikan 1 pada persamaan (1) sehingga diperoleh:

3x + 2y + z = 20  |x2     6x + 4y + 2z = 40

x + 4y + 2z = 15  |x1           x + 4y + 2z = 15 –

5x              = 25