Pertidaksamaan Linear Satu Variabel

Pertidaksamaan Linear Satu Variabel – Dalam matematika kita mempelajari persamaan dan pertidaksamaan. Kali ini kita bahas pertidaksamaan linear satu variabel. Kita bahas satu per satu, yang diawali dari definisinya terlebih dahulu.

Apa itu Pertidaksamaan Linear Satu Variabel (SPtLSV)

Pertidaksamaan linear satu variabel adalah pertidaksamaan yang memiliki satu variabel dan memiliki pangkat satu, serta memakai tanda ketidaksamaan. Yang dimaksud tanda ketidaksamaan adalah “>”, “ ≥ ”, “<“, dan “≤”.

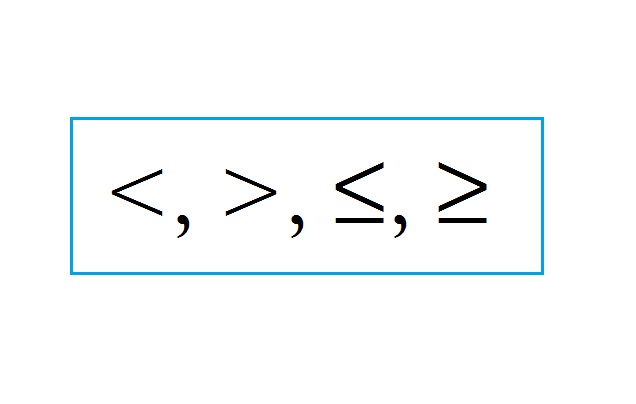
Di samping itu persamaan linear satu variabel juga dapat diartikan sebagai suatu kalimat atau pernyataan terbuka yang mempunyai variabel, eksponen atau pangkat satu dan mempunyai hubungan >, <, > atau ≤.

Pertidaksamaan linear satu variabel mempunyai bentuk yang cukup beragam. Antara lain ax + b < 0, ax + b > 0, ax + b > 0, atau ax + b <0. Dalam penulisannya ada dua syarat yang harus terpenuhi. Yakni a ≤ 0, serta a dan b adalah bilangan nyata (real).

Baca juga: Pertidaksamaan Linear Dua Variabel

Langkah Mengerjakan Pertidaksamaan Linear Satu Variabel

1. Sederhanakan terlebih dahulu operasi yang ada. Berlaku juga pada operasi bertanda kurung.
2. Gabungkan suku yang mengandung variabel ke dalam satu ruas.
3. Menambahkan atau mengurangi kedua ruas dengan bilangan yang sama tanpa mengubah tanda ketidaksamaan.
4. Mengalikan atau membagi kedua ruas dengan bilangan positif yang sama tanpa mengubah tanda ketidaksamaan.
5. Mengalikan atau membagi kedua ruas dengan bilangan negatif yang sama, tapi tanda ketidaksamaannya berubah, dimana:
   1. > menjadi < , dan sebaliknya
   2. < menjadi > , dan sebaliknya

Pada pertidaksaman linear satu variabel kita dapat mengerjakannya dengan memanfaatkan metode substitusi. Kita bisa melakukan operasi perhitungan seperti penjumlahan, pengurangan, perkalian, dan pembagian. Bahkan kita juga bisa membagi ruas pertidaksamaan dengan bilangan yang sama.

Sifat Pertidaksamaan Linear Satu Variabel

Pertidaksamaan linear satu variabel mempunyai beberapa sifat yang harus kita pahami. Berikut beberapa sifat tersebut:

1. Ax + Cx < Bx + Cx
2. Ax – Cx < Bx – Cx
3. Ax x Cx < Bx x Cx, bila C > 0 untuk semua x
4. Ax x Cx > Bx x Cx, bila C < 0 untuk semua x
5. Ax /Cx < Bx/Cx, bila C > 0 untuk semua x
6. Ax/Cx > Bx/Cx, bila C < 0 untuk semua x

Ketentuan di atas pun berlaku untuk tanda >  atau <

Baca juga: Persamaan Linear Satu Variabel, Rumus Dan Contoh Soal

Menyelesaikan Pertidaksamaan Linear Satu Variabel

Selain memakai metode substitusi, masih ada dua cara lain untuk mengerjakan soal PtLSV. Yakni dengan cara ekuivalen dan pindah ruas. Seperti apa penjelasan 3 metode tersebut? Simak penjelasan singkatnya di bawah ini.

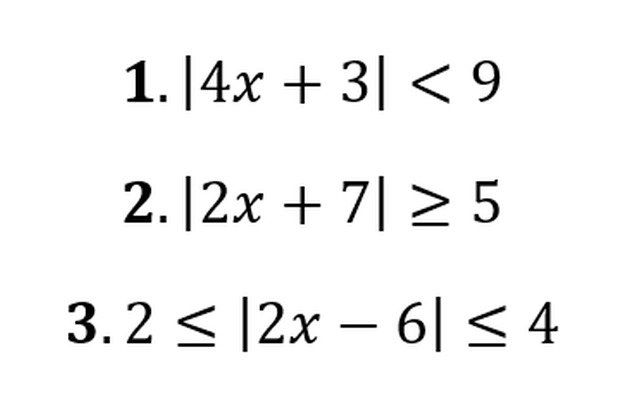
Substitusi

Sesuai dengan namanya, substitusi dilakukan dengan mengganti sembarang x dan dimasukkan ke dalam pertidaksamaan untuk memperoleh pernyataan yang benar. Hanya saja cara ini dinilai kurang efektif. Sebab kita harus melakukan sejumlah percobaan sampai ditemukan hasil yang sesuai.

Ekuivalen

Pada cara ini ada dua opsi yang bisa dilakukan. Pertama, kita bisa menambah dan mengurangi dengan bilangan yang sama, melakukan operasi perkalian atau pembagian dengan bilangan positif dan tidak mengubah tanda pertidaksamaan.

Cara kedua adalah mengalikan atau membagi dengan bilangan negatif, serta mengubah tanda pertidaksamaan menjadi kebalikannya. Contohnya < berubah menjadi >.

Pindah Ruas

Pindah dilakukan dengan memindahkan bilangan yang ada di sisi kanan atau kiri tanda pertidaksamaan menjadi ke sisi sebelahnya. Dengan begitu bilangan-bilangan tersebut bisa kita hitung dan ketahui hasil akhirnya.

Contoh Soal

Soal 1 (Metode Subtitusi)

Selesaikan contoh soal pertidaksamaan berikut ini:

5x + 2 > 12

Jawab :

Jika x = 1 maka 5 (1) + 2   > 12

5 + 2      > 12

7    > 12 (salah)

Jika x = 3 maka 5 (3) + 2   > 12

15 + 2    > 12

17  > 12 ( pernyataan benar )

Untuk cara pertama ini, kurang efektif karena harus melakukan beberapa percobaan terlebih dahulu. Cara yang paling cepat gunakan cara ke dua atau ketiga yang akan dijelaskan dibawah ini.

Soal 2 (Metode Ekuivalen)

Selesaikan contoh soal pertidaksamaan berikut ini:

2x – 1 > 4 x + 5

Jawab :

= 2x – 1 + 1 > 4 x + 5 + 1 ( kedua ruas di tambah 1 dan tidak mengubah tanda)

= 2x > 4x + 6

= 2x – 2x > 4x – 2x + 6 (kedua ruas dikurangi 2x)

= -2x > 6

= -2x / -2 > 6/ -2 (kedua ruas dibagi -2 dan mengubah tanda )

= x < -3

Soal 3 (Metode Pindah Ruas)

Selesaikan contoh soal pertidaksamaan berikut ini.

Contoh 1.1 : 6 (x – 3) > 2x + 5

Jawab :

= 6x – 18 > 2x + 5

= 6x – 2x > 18 + 5

= 4x > 22

= x > 22/4

= x > 5,5

Contoh 1.2 : Himpunan penyelesaian dari 5x – 5 > 10 dengan x anggota bilangan asli adalah

Jawab :

5x – 5 > 10

5x > 10 + 5