Pertidaksamaan Linear Dua Variabel – Dalam materi program linear ada beberapa jenis pertidaksamaan yang bisa kita pelajari. Seperti pertidaksamaan linear satu variabel dan pertidaksamaan linear dua variabel. Kini kita bahas lebih lanjut mengenai pertidaksamaan linear dua variabel.
Pertidaksamaan linear dua variabel (SPtLDV) tidak bisa disamakan dengan persamaan linear dua variabel (SPLDV). Karena keduanya mempunyai tanda hubung yang berbeda. Begitu juga dengan cara mengerjakannya. Pada kesempatan ini kita bahas lebih jauh seputar pertidaksamaan linear dua variabel.
Apa itu SPtLDV
Kita awali dengan mengenal sistem pertidaksamaan linear dua variabel lebih dekat. Supaya lebih mudah dipahami kita pahami arti pertidaksamaan terlebih dahulu. Pertidaksamaan adalah bentuk atau kalimat matematis yang memiliki tanda penghubung seperti lebih dari (>), kurang dari (<), lebih dari atau sama dengan (>=), ataupun kurang dari atau sama dengan (<=).
Sedangkan linear merupakan bentuk aljabar dimana variabelnya memiliki pangkat tertinggi 1. Dari dua definisi tersebut dapat kita ketahui bahwa pertidaksamaan linear dua variabel adalah sebuah bentuk pertidaksamaan yang mempunyai dua variabel dengan pangkat tertinggi dari variabelnya adalah 1.
Setelah mengetahui apa itu SPtLDV, kita kenali bentuk umum dari pertidaksamaan ini. Ada beberapa bentuk yang bisa kita amati, antara lain:
- ax + by > c
- ax + by < c
- ax + by >= c
- ax + by <= c
Dimana:
- a, b : koefisien
- x, y : variabel
- c : konstanta
- >, <, >=, <= : tanda pertidaksamaan
Baca juga: Materi Pertidaksamaan Linear Satu Variabel
Penyelesaian Pertidaksamaan Linear Dua Variabel

Sudah dijelaskan bahwa pertidaksamaan linear dua variabel ini merupakan gabungan dari beberapa pertidaksamaan linear dua variabel. Sehingga untuk menyelesaikannya kita perlu mengubah hal-hal yang berkaitan dengan dua variabel tersebut. Ada beberapa langkah untuk mengerjakan PtLDV, antara lain:
- Ubah tanda pertidaksamaan menjadi tanda sama dengan (=).
- Cari nilai dari titik x saat y = 0 dan sebaliknya.
- Gambar grafik garis yang menghubungkan kedua titik.
- Arsir daerah yang bersesuaian dengan tanda pertidaksamaan.
Baca juga: Materi Persamaan Linear Satu Variabel
Contoh kasus agar materi ini lebih mudah untuk dipahami:
Sebuah gerobak hanya bisa membawa beban kurang dari 20 kg. Satu keranjang apel memiliki berat sebesar 4 kg dan satu keranjang mangga memiliki berat sebesar 1 kg. Berapa keranjang apel dan mangga yang dapat dibawa oleh 1 buah gerobak? minimum harus lebih dari 10 keranjang!
Jawab:
Soal cerita di atas adalah salah satu dari bentuk pertidaksamaan. Mengapa demikian? Kata kunci dari bentuk pertidaksamaan adalah lebih dari atau kurang dari. Jika diubah ke dalam bentuk model matematika, soal cerita di atas akan menjadi:
4x + y < 20
x + y >= 10
Berikut ini merupakan langkah-langkah untuk menyelesaikan pertidaksamaan di atas:
Langkah 1: mencari nilai dari titik x saat y = 0 dan sebaliknya
Terlebih dahulu pertidaksamaan di atas kita ubah menjadi bentuk persamaan, yaitu:
4x + y < 20 dan x + y >= 10
Pertidaksamaan 1:
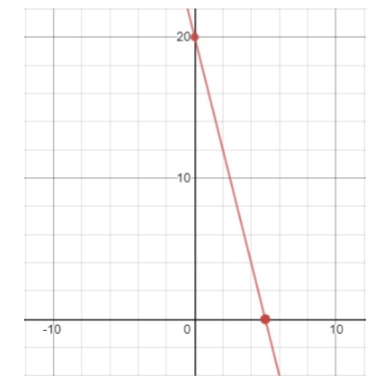
Saat y = 0 maka 4x = 20 sehingga x = 5
Saat x = 0 maka y = 20
Sehingga diperoleh titik-titik (5, 0) dan (0, 20)
Pertidaksamaan 2:
Saat y = 0 maka x = 10
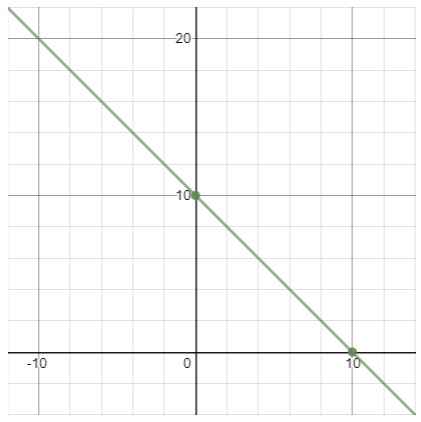
Saat x = 0 maka y = 10
Sehingga diperoleh titik-titik (10, 0) dan (0, 10)
Langkah 2: Menggambar grafik garis yang menghubungkan kedua titik
Pertidaksamaan 1:
Berikut ini merupakan grafik garis yang menghubungkan titik (5, 0) dan (0, 20):
Pertidaksamaan 2:
Berikut ini merupakan grafik garis yang menghubungkan titik (10, 0) dan (0, 10)