Rumus Transformasi Geometri – Geometri menjadi materi penting dalam matematika karena penerapannya dapat berguna untuk kehidupan. Selain menjadi materi dalam matematika, pemahaman geometri juga dapat bermanfaat untuk bidang ilmu lain, seperti kimia dan fisika.
Geometri merupakan cabang ilmu matematika yang menerangkan sifat-sifat dari sebuah garis, sudut, bidang, hingga ruang sebuah bidang. Pada bidang datar, materi geometri memiliki berbagai macam jenis pembelajaran untuk menerangkan rumus-rumus di segala bidangnya. Pemahaman geometri bidang akan bermanfaat dalam pembelajaran geometri ruang.
Geometri sendiri dapat memiliki tranformasi. Transformasi geometri itu berhubungan dengan perubahan rupa yang dilihat dari garis, sedut, bidang, dan ruang. Kalau dalam pelajaran matematika, transformasi geometri posisi awal bidang dinotasikan dengan (x, y) dan posisi akhir dinotasikan dengan (x’,y’).
Pada pembahasan kali ini, kalian akan mempelajari mengenai transformasi geometri. Berikut penjelasannya.
Jenis-jenis Transformasi Geometri
Transformasi geometri adalah proses mengubah setiap titik koordinat menjadi titik koordinat lain pada bidang tertentu. Transformasi bisa juga dilakukan pada kumpulan titik yang membentuk bidang/bangun tertentu. Jika sobat punya sebuah titik A (x,y) kemudian ditransformasikan oleh transformasi T dapat menghasilkan titik yang baru A’ (x’,y’).
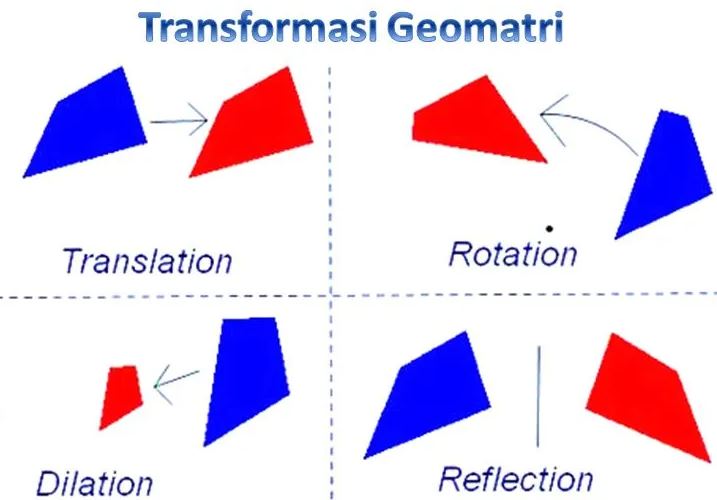
Di dalam transformasi geometri dikenal adanya 4 jenis transformasi yang bisa dilakukan terdapat sebuah koordinat yaitu menggesernya, mencerminkannya, memutar, memperbesar, atau mengecilkan. Selain 4 transformasi tersebut masih ada yang namanya regangan dan gusuran.
1. Translasi
Translasi atau pergeseran adalah transformasi yang memindahkan setiap titik pada bidang menurut jarak dan arah tertentu. Sobat bisa mengatakan kalau translasi hanya memindahkan tanpa mengubah ukuran tanpa memutar. Kata kuncinya transformasik ke arah yang sama dan ke jarak yang sama. Misalnya, ada sebuah titik T (x,y) yang ditranslasikan menurut (a,b) maka hasil setelah transfromasi sebagai berikut.

2. Refleksi
Refleksi atau sering disebut dengan istilah pencerminan adalah suatu transformasi dengan memindahkan setiap titik pada bidang dengan menggunakan sifat-sifat pencerminan pada cermin datar. Dengan kesimpulan rumusnya sebagai berikut.
- Pencerminan terhadap sumbu -x : (x,y) → (x, -y)
- Pencerminan terhadap sumbu -y : (x,y) → (-x, y)
- Pencerminan terhadap garis y = x : (x,y) → (y,x)
- Pencerminan terhadap garis y = x : (x,y) → (-y, -x)
- Pencerminan terhadap garis x = k : (x,y) → (2k -x,y)
- Pencerminan terhadap garis y = k : (x,y) → (x, 2k – y)
3. Rotasi
Rotasi adalah memutar setiap titik pada bidang dengan menggunakan titik pusat tertentuk yang memiliki jarak sama dengan setiap titik yang diputar (jari-jari). Rotasi tidak mengubah ukuran benda sama sekali. Ada dua macam rotasi, rotasi dengan titik pusat (0,0) dan rotasi dengan titik tertentu P (a,b).
Baca juga: Pengertian dan Kegunaan Neraca Ohaus




