Contoh Soal Geometri Bidang Datar Dan Jawaban

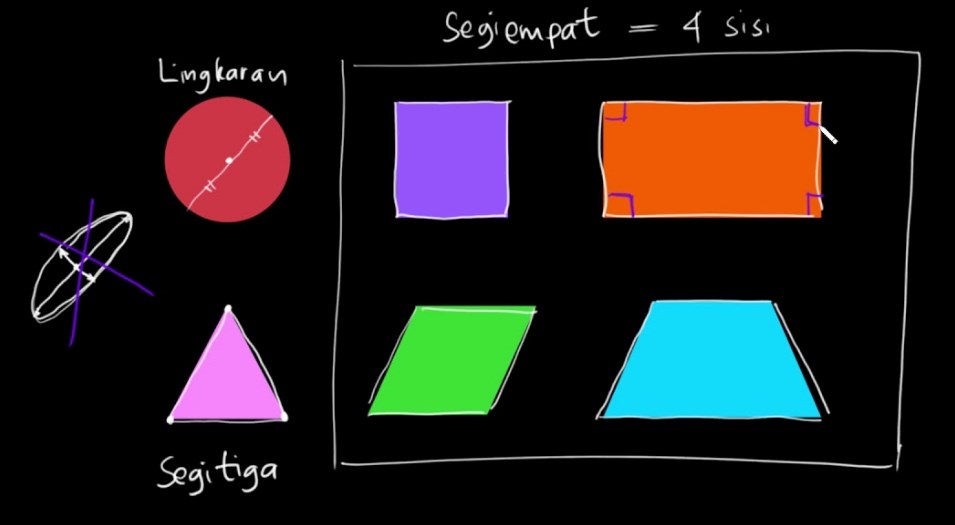
Contoh Soal Geometri Bidang Datar – Banyak ilmu matematika yang telah dikenal sejak dahulu dan sangat berguna untuk kehidupan sehari-hari. Salah satunya adalah cabang ilmu geometri. Geometri menjadi materi penting dalam matematika karena penerapannya dapat berguna untuk kehidupan. Selain menjadi materi dalam matematika, pemahaman geometri juga dapat bermanfaat untuk bidang ilmu lain, seperti kimia dan fisika.

Geometri merupakan cabang ilmu matematika yang menerangkan sifat-sifat dari sebuah garis, sudut, bidang, hingga ruang sebuah bidang. Pada bidang datar, materi geometri memiliki berbagai macam jenis pembelajaran untuk menerangkan rumus-rumus di segala bidangnya. Pemahaman geometri bidang akan bermanfaat dalam pembelajaran geometri ruang.

Pada pembahasan kali ini, kalian akan mempelajari mengenai geometri pada bidang datar. Tentunya, agar pemahaman dapat diaplikasikan dengan baik pelajarilah beberapa latihan soal dengan pembahasannya di bawah ini.

Baca juga: Cara Mencari Panjang Sisi Segitiga Lengkap

Baca juga: Rumus Kesebangunan Bangun Datar

Pengertian Geometri Bidang Datar

Geometri menjadi cabang matematika yang sudah diterapkan sejak zaman dahulu dan menjadi yang paling tua dalam sejarah. Beberapa ilmuwan terdahulu sudah pernah mempelajari geometri, seperti Phytagoras, Thales, Euclid, dan sebagainya.

Geometri merupakan bagian dari ilmu matematika yang menjelaskan mengenai hubungan dari titik, garis, bangun, dan sudut. Empat objek dalam geometri ini akan memberikan hubungan untuk memperoleh sebuah perhitungan, seperti mengukur luar daerah atau keliling sebuah benda.

Hal ini pun menjadi bahasan utama untuk mempelajari geometri bidang datar yang merupakan kumpulan dari beberapa garis yang saling berhubungan. Dengan begitu, dapat dipahami bahwa sebuah geometri bidang datar merupakan suatu bentuk geometris yang memiliki dua dimensi. Hal ini karena bangun datar hanya memiliki luas saja dan tidak memiliki volume.

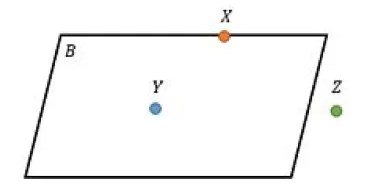
Bagian paling dasar pada bidang datar ditunjukkan dengan adanya titik. Titik biasanya terletak pada garis dan dapat dibedakan dengan titik dalam dan titik luar. Berikut contoh peletakan titik X, Y, dan Z dengan titik X dan Y berada di bidang, sedangkan titik Z ada di luar bidang B.

Dari titik, kita dapat melihat kedudukan garis pada bidang. Garis biasanya terbagi menjadi empat, yaitu saling sejajar, berpotongan, berimpit, dan bersilang. Biasanya, dua garis akan disebut saling sejajar apabila di bidang yang sama, tidak memiliki titik potong, dan jarak antar-garis selalu tetap.

Lalu, dua garis akan disebut saling berpotongan apabila ada bidang sama dan saling bertemu pada salah satu titik. Selanjutnya, untuk dua garis saling bersilang terjadi pada bidang yang sama, tidak berpotongan, dan tidak saling sejajar.

Setelah mengetahui titik dan garis pada sebuah bidang datar, selanjutnya kalian harus mengetahui hubungan antar-sudutnya. Sudut pada bidang datar terbagi menjadi empat, yaitu sudut saling berpenyiku, berpelurus, bertolak belakang, dan dua garis sejajar yang dipotong garis yang lain.

Baca juga: Sifat-Sifat Semua Bangun Datar Lengkap

Rumus Geometri Bidang Datar

Dasar-dasar dari geometri bidang datar yang terdiri atas titik, garis, dan sudut selanjutnya dapat dioperasikan lebih lanjut untuk mengetahui beberapa rumus dasar untuk mencari luas dan keliling sebuah bangun datar. Berikut penjelasannya.

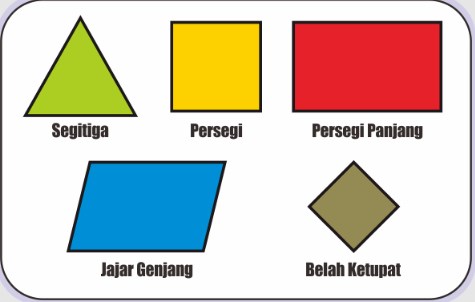
1. Persegi

Persegi dapat disebut sebagai bujur sangkar dan memiliki empat sisi yang sama panjang. Persegi juga memiliki empat sudut yang sama berbentuk siku-siku.

Rumus keliling: K = 4.s

Rumus luas: L = s x s atau s²

2. Persegi panjang

Persegi panjang merupakan bangun datar yang mirip dengan bujur sangkar, namun memiliki empat sisi dengan dua sisinya yang saling berhadapan. Keempat sudutnya berbentuk sudut siku-siku.

Rumus keliling: K = 2p + 2l

Rumus luas: L = p x l

3. Segitiga

Segitiga merupakan bangun datar yang memiliki total sudut sebesar 180⁰ dengan menghubungkan tiga titik yang tidak segaris. Segitiga memiliki beberapa jenis, yaitu segitiga sama kaki, segitiga sama sisi, segitiga siku-siku, dan segitiga sembarang.

Rumus keliling: K = 3.s

Rumus luas: L = ½ x alas x tinggi

4. Jajar genjang

Jajar genjang merupakan bangun datar yang memiliki dua pasang sisi sejajar.

Rumus keliling: K = 2 (p + l)

Rumus luas: L = alas x tinggi

5. Belah ketupat

Belah ketupat merupakan bangun datar dengan dua pasang sisi yang sama panjang.

Rumus keliling: 4 x s

Rumus luas: L = ½ . d1. d2

Baca juga: Rumus Luas Dan Keliling Bangun Datar

Contoh Soal

Setelah mempelajari sekilas mengenai geometri bangun datar, pahamilah beberapa contoh soal berikut beserta jawabannya agar lebih menguasai materi ini.