Rumus Integral Subtitusi dan Contoh Soal

Misalnya, kita menemukan persoalan integral tertentu dengan interval a ≤ b ≤c tertentu dan harus disubtitusikan ke dalam interval yang baru bagi variabel U pada contoh soal f₀² (x⁴ + 5)³ x³ dx.

Baca juga: Rumus Integral Parsial dan Contoh Soal

Integral Subtitusi pada Fungsi Trigonometri

Dalam penerapannya, trigonometri dapat dijadikan sebuah kebalikan dari turunan dan dibahas pada materi integral trigonometri. Perlu kita ingat bahwa integral sendiri merupakan kebalikan dari sebuah turunan. Dengan begitu, integral trigonometri menjadi kebalikan dari turunan trigonometri. Beberapa persoalan mengenai integral fungsi trigonometri dapat diperoleh berdasarkan informasi bahwa integral trigonometri dapat dijadikan sebagai suatu anti turunan.

Pada beberapa persoalan, trigonometri dapat dijadikan sebagai integran dan tidak dapat langsung diintegralkan seperti persoalan rumus pada fungsi aljabar yang disubtitusikan. Hal ini karena pada trigonometri perlu disesuaikan perubahan fungsinya sehinga terdapat sebuah persamaan.

Berikut beberapa perubahan fungsi trigonometri yang perlu dipelajari.

Setelah menyelaraskan perubahan fungsi trigonometrinya, integral trigonometri dapat diselesaikan dengan metode subtitusi layaknya operasi perhitungan integral pada fungsi aljabar. Hal ini dapat dilakukan dengan rumus subtitusi jika integran terdiri atas perkalian fungsi dengan fungsi turunan. Pengoperasiannya pun dapat seperti aljabar dengan menggunakan pemisalan. Misalnya, soal 2x sin (x² + 1) dx.

Hasil integral dapat disubtitusikan dengan pemisalan U menjadi – cos U + C = – cos (x² + 1) + C.

Integral Subtitusi dengan Integran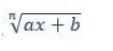

Teknik subtitusi ini dapat dimisalkan dengan yⁿ = ax + b pada penyelesaian integral pada fungsi f (y) menggunakan teknik substitusi seperti aljabar. Misalnya seperti berikut.

Integral juga dapat berintegran dengan akar seperti berikut.

Baca juga: Cara Menghitung Volume Kerucut Yang Benar

Contoh Soal

Setelah mempelajari beberapa pembahasan mengenai integral subtitusi di atas, perlu lah kalian memahami lebih lanjut dengan mempelajari contoh-contoh soal berikut beserta pembahasannya.

1.