Rumus Integral Trigonometri dan Contoh Soal – Seiring berkembangnya zaman, pemanfaatan integral sudah berkembang dengan luas dan dapat diaplikasikan dengan sudut pandang keilmuan matematika. Sudut pandang ini dapat ditelaah dengan pemanfaatan ilmu aljabar pada integral dengan adanya operasi invers dari operasi turunan. Lalu, terdapat pemanfaatan dalam geometri dengan metode integral untuk mencari luas sebuah daerah yang limit dari jumlahnya. Salah satunya dengan pembahasan trigonometri pada sebuah integral.
Jika berbicara mengenai trigonometri, hal yang terlintas adalah mengenai sudut-sudut segitiga dengan sin, cos, tan-nya. Trigonometri sendiri menjadi salah satu ilmu matematika yang membahas mengenai relasi antara sisi dan sudut dalam segitiga. Konsep trigonometri menjadi salah satu hal yang penting untuk dipelajari lebih dalam karena dapat diaplikasikan pada beberapa materi lainnya di matematika.
Salah satu materi yang mengaplikasikan trigonometri pada pembahasannya adalah integral. Sebelumnya, jika kita melihat aspek integral biasanya berhubungan dengan operasi aljabar. Namun, dalam penerapannya trigonometri dapat dijadikan sebuah kebalikan dari turunan dan dibahas pada materi integral trigonometri. Perlu kita ingat bahwa integral sendiri merupakan kebalikan dari sebuah turunan. Dengan begitu, integral trigonometri menjadi kebalikan dari turunan trigonometri. Beberapa persoalan mengenai integral fungsi trigonometri dapat diperoleh berdasarkan informasi bahwa integral trigonometri dapat dijadikan sebagai suatu anti turunan.

Baca juga: Rumus Integral, Jenis, dan Pembahasan
Baca juga: Rumus Integral Tertentu dan Tak Tentu
Pada pembahasan kali ini, kalian akan mempelajari mengenai salah satu materi integral yang membahas mengenai trigonometri yaitu integral trigonometri. Berikut pembahasannya.
Pengertian Integral Trigonometri
Integral trigonometri atau dapat disebut sebagai integral fungsi trigonometri merupakan proses penghitungan integral yang memuat fungsi integral. Perlu diingat kembali bahwa integral menjadi sebuah invers atau kebalikan dari turunan fungsi. Integral juga dapat dimaknai sebagai kalkulus integral yang disimbolkan dengan fungsi (F) yang merupakan anti dari turunan. Hal ini didasari pada integral dari fungsi (f) pada selang (I) dan jika F (x) = f (x) akan berlaku untuk setiap “x” atau “I”. Maksudnya, kita dapat memahaminya dengan sederhana seperti saat mendengar istilah aljabar mengenai invers atau kebalikan.
Dengan begitu, dalam proses penentuan integral trigonometri tentu tidak jauh beda dengan pengoperasian perhitungan integral-integral lainnya, seperti integral tentu, integral tak tentu, dan lain sebagainya. Bedanya, dalam integral trigonometri menerapkan fungsi trigonometri seperti pembahasan sin, cos, dan tan.
Umumnya, integral menggunakan fungsi aljabar dan dapat dioperasikan pada suatu fungsi trigonometri. Beberapa integral fungsi trigonometri dapat diperoleh dengan mudah berdasarkan informasi bahwa integral merupakan anti turunan atau kebalikan dari turunan, yakni . Dapat dimaknai bahwa fungsi f(x), diturunkan atau didiferensialkan maka akan diperoleh suatu fungsi baru sebagai f'(x). Jika fungsi baru hasil turunan dari f(x) diintegralkan berarti kita akan memperoleh fungsi f(x) itu sendiri.
Baca juga: Rumus Integral Parsial
Pada sebuah fungsi trigonometri yang dijadikan sebuah integral membutuhkan perubahan integral dalam penyelesaiannya. Hal tersebut dilakukan karena fungsi trigonometri tidak dapat langsung diselesaikan menggunakan integral awal. Namun, sama seperti penghitungan permasalahan integral yang lain, integral trigonometri dapat diselesaikan dengan metode integral substitusi atau integral parsial.
Oleh karena itu, dalam penghitungan integral trigonometri perlu menggunakan perubahan fungsi trigonometri dalam pengintegralan substitusinya yang dapat dipahami seperti berikut.
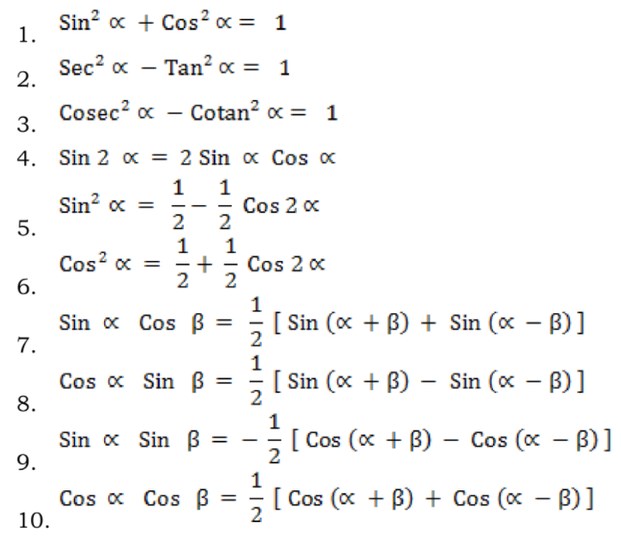
Rumus Integral Trigonometri
Perlu diingat bahwa dalam penyelesaian masalah integral trigonometri kita perlu mengelola fungsi trigonometri baku terlebih dahulu. Selain itu, kalian juga harus mengetahui fungsi identitas trigonometrinya. Hal ini digunakan untuk menyederhanakan fungsi trigonometri menjadi bentuk yang tepat sehingga lebih mudah untuk menentukan nilai trigonometrinya.





