Rumus Integral Subtitusi dan Contoh Soal

Rumus Integral Subtitusi dan Contoh Soal – Jika membahas mengenai materi integral, kita akan disuguhkan dengan berbagai macam jenisnya yang harus disesuaikan dengan rumus-rumus terkait. Meskipun terlihat rumit dan membutuhkan proses panjang, integral memberikan kemudahan bagi kehidupan kita, khususnya dalam memecahkan masalah matematika yang rumit. Namun, dalam membahas mengenai integral kita perlu memahami dasar-dasarnya seperti pembahasan kalkukus dan diferensial atau turunan. Hal ini menjadi dasar karena berkaitan dengan pemahaman mengenai integral.

Dalam memecahkan masalah matematika menggunakan integral, terdapat berbagai metode dan rumus-rumus dasarnya. Salah satunya dengan melakukan metode subtitusi pada persoalan integral. Integral subtitusi ini dapat menjadi dasar atau kunci ketika kita dihadapkan dengan soal-soal integral. Rumus integral substitusi dapat digunakan ketika bagian dari sebuah fungsi merupakan turunan dari fungsi lainnya. Biasanya, soal integral yang dapat diselesaikan menggunakan cara substitusi terdiri dari 2 faktor dengan turunan dari salah satu faktornya memiliki hubungan dengan faktor lainnya.

Penerapan integral subtitusi sendiri dapat digunakan pada berbagai tipe soal integral. Misalnya, dalam penerapan fungsi aljabar integral dan trigonometri kita dapat memanfaatkan metode subtitusi untuk menyelesaikan soal-soalnya. Oleh karena itu, pemahaman dasar mengenai metode subtitusi dalam pengerjaan materi integral sangat dibutuhkan dan perlu dipahami dengan baik.

Baca juga: Rumus Integral, Jenis, dan Pembahasan

Baca juga: Rumus Integral Trigonometri dan Contoh Soal

Pada pembahasan kali ini, kalian akan mempelajari mengenai materi rumus integral yang menggunakan metode subtitusi dalam pengerjaannya. Selain itu, untuk memperkuat pemahaman kalian terdapat beberapa contoh soal dan pembahasannya pula. Berikut pembahasannya.

Pengertian Integral Subtitusi

Integral merupakan kebalikan dari turunan yang memiliki makna menurunkan sebuah fungsi f (x) yang dapat kita pahami bahwa integral adalah bentuk penjumlahan yang disusun kontinu dan terdiri atas anti turunan. Integral yang menjadi kebalikan turunan memiliki faktor yang merupakan turunan dari faktor lainnya sehingga dalam pengerjaannya dapat menggunakan metode umum, yaitu metode subtitusi.

Integral subtitusi sendiri merupakan sebuah cara atau metode yang digunakan untuk mencari suatu integral dengan cara menyubtitusikan salah satu variabel dan mengubahnya menjadi sebuah bentuk yang lebih sederhana. Ciri-ciri soal dalam integral yang dapat diselesaikan menggunakan metode subtitusi adalah persoalan integral dengan bagian fungsinya adalah turunan dari fungsi lainnya.

Integral sendiri diartikan sebagai objek matematika yang bisa didefinisikan sebagai area atau generalisasi. Integral berkaitan dengan turunan sebagai objek dasarnya. Namun, dalam penerapannya terdapat rumus umum yang dapat dijadikan dasar penghitungannya. Rumus umum yang dapat digunakan dalam pengerjaan persoalan integral menggunakan metode subtitusi dapat dilihat sebagai berikut.

Selain menggunakan rumus di atas, perlu diingat bahwa persoalan-persoalan integral memiliki berbagai macam jenisnya. Dengan begitu, kita perlu memperhatikan apakah jenis soal integral yang ditampilkan dapat diselesaikan dengan rumus subtitusi secara umum.

Baca juga: Rumus Integral Tertentu dan Tak Tentu

Integral Subtitusi pada Fungsi Aljabar

Aljabar merupakan salah satu cabang ilmu matematika yang menggunakan simbol dan operasi matematika. Seperti halnya operasi bilangan dalam matematika, aljabar berhubungan sangat erat dengan operasi penjumlahan, pengurangan, perkalian, pembagian, hingga perpangkatan. Namun, aljabar sendiri dapat memiliki faktor turunan yang dibalikkan dan disebut sebagai integral pada fungsi aljabar.

Integral pada fungsi aljabar dapat diselesaikan menggunakan beberapa rumus, salah satunya dengan metode subtitusi. Rumus integral subtitusi pada fungsi aljabar harus memiliki faktor turunan dari faktor lainnya. Berdasarkan teknik integral subtitusi pada fungsi aljabar dapat kita telaah bahwa f(x) dapat diubah dalam bentuk k.(g(x)ⁿ.g^I(x). Agar lebih paham penerapan fungsi aljabar pada sebuah integral akan ditampilkan contoh soal sebagai berikut.

Perhatikan

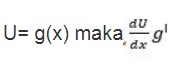
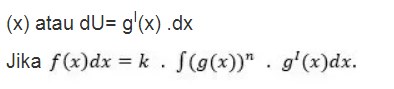
Integral di atas dapat diselesaikan penggunaan pemisalan U = g(x) dan U = g^I(x) dengan persamaan sebagai berikut.