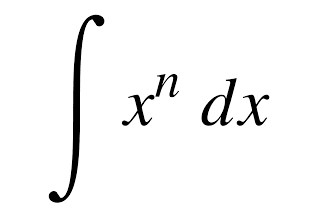Rumus Integral Tertentu dan Tak Tentu – Tentunya kita telah mengetahui bahwa konsep integral adalah kebalikan dari pendeferensialan. Dengan begitu, pada integral dapat kita pahami mengenai fungsi umum yang bersifat F(x) memiliki makna himpunan anti-turunan atau himpunan pengintegralan. Jadi, secara tidak langsung integral dapat bermakna sebuah konsep penjumlahan yang berkesinambungan dalam matematika. Dengan perkembangan konsep integral, kita dapat memanfaatkannya dalam setiap permasalahan matematika yang berhubungan dengan kebalikan dari turunan.
Dalam pembahasan integral, kita perlu mengetahui jenis-jenisnya. Beberapa jenis dari rumus integral dapat memberikan kemudahan kita untuk menyelesaikan permasalahan pada integral. Dari beberapa jenis integral sendiri, terdapat hal umum yang perlu diketahui lebih dalam untuk menyelesaikan permasalahan integral dengan mempelajari integral tentu dan tak tentu. Kedua jenis integral ini saling berkaitan dan perlu dipelajari dengan detil untuk meningkatkan pemahaman dalam memecahkan permasalahan integral.
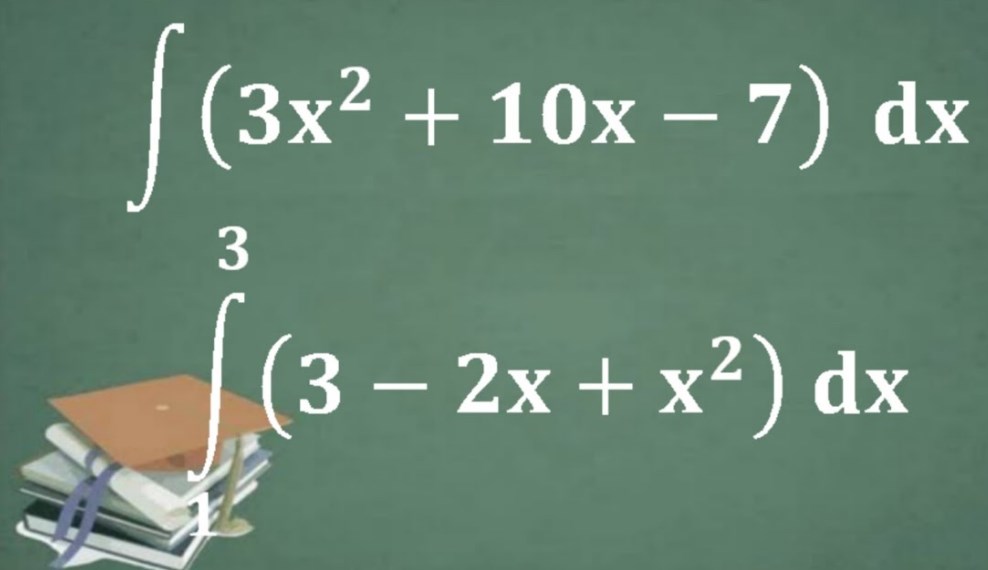
Baca juga: Rumus Integral, Jenis, dan Pembahasan
Sebelum membahas lebih jauh mengenai integral tentu dan tak tentu, sebaiknya kalian dapat mengingat kembali mengenai beberapa cabang materi matematika yang lain seperti turunan. Misalnya, turunan fungsi aljabar y = x3 diturunkan menjadi yI = 3x2 . Bahan turunan tersebut mempunyai persamaan dalam hasil turunannya. Variabel x³ pada sebuah fungsi baik dikurangi ataupun ditambah bilangan (seperti -6, +8, +17) memperoleh hasil turunan yang sama. Turunan tersebut lalu diintegralkan dan alhasil akan sama ibarat fungsi awal sebelum proses penurunan. Penyelesaian tersebut memakai rumus integral yang ada.
Baca juga: Rumus Integral Parsial dan Contoh Soal
Pada pembahasan kali ini, kalian akan mempelajari mengenai jenis integral tentu dan tak tentu beserta contoh soal dan pembahasannya. Berikut penjelasannya.
Pengertian Integral Tentu
Integral tentu mulanya dipopulerkan oleh ilmuwan yang bernama Leibinz dan Newton dengan pembahasan lebih lanjut oleh Riemann dengan memperkenalkan integral secara modern. Pada dasarnya perhitungan integral tentu dapat digunakan untuk menghitung volume benda saat diputar ataupun luas bawah kurva yang disertai batas tertentunya. Perhitungan ini sanggup memakai rumus integral tentu ataupun aplikasi integral.
Integral tentu memiliki pengertian yang berhubungan dengan nilainya yang telah ditentukan di awal dan akhirannya. Hal ini berhubungan dengan rentang batas atas dan bawah sebuah integral. Jenis integral tentu merupakan integral yang memiliki batas dengan suatu nilai konstanta dan bisa disimbolkan dengan variabel. Dalam mencari nilai atas integral tentu dapat melakukan subtitusi batas atas ke fungsi hasil integral dan hasil batas bawah di fungsi hasil integral. Bentuk dari integral tentu ditunjukkan sebagai berikut.
Pada integral tentu, dapat kita perhatikan penggambaran grafiknya seperti berikut.

Selain dengan penggambaran grafik di atas, integral tentu memiliki beberapa sifat dasarnya sebagai berikut.
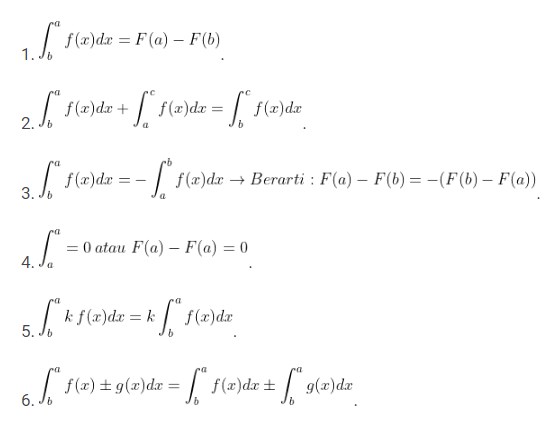
Baca juga: Rumus Integral Trigonometri dan Contoh Soal
Pengertian Integral Tak Tentu
Integral tak tentu menjadi sebuah anti turunan atau kebalikan dari sebuah turunan. Integral sendiri memiliki fungsi dalam menentukan daerah, volume, titik pusat, dan lainnya. Kalau suatu fungsi f(x) dibalik menjadi f’(x) maka itu merupakan turunan. Akan tepati, jika f’(x) dibalik lagi menjadi f(x) menjadikan fungsi tersebut adalah sebuah integral.
Fungsi ini dibaca “integral tak tentu dari fungsi f(x) terhadap variabel x.”
Dengan begitu, integral tak tentu dapat memiliki makna mengenai suatu fungsi baru yang punya turunan dari fungsi aslinya dan fungsi tersebut belum memiliki nilai pasti. Dengan begitu, dalam integral tak tentu ada sebuah konstanta (C).
Pada integral tak tentu dapat diketahui melalui grafik yang digambarkan sebagai berikut.