Rumus Integral Parsial dan Contoh Soal

Rumus Integral Parsial dan Contoh Soal – Jika berbicara mengenai integral, tentunya perlu hal-hal dasar yang harus dipahami untuk menyelesaikan soal-soalnya. Pembahasannya pun sudah diterapkan dari bangku sekolah dengan pembelajaran sebelumnya yang berhubungan dengan kalkukus dan diferensial atau turunan. Dengan adanya pembahasan mengenai integral, akan dapat diterapkan aplikasinya untuk membantu kita dalam menyelesaikan sebuah masalah dalam kehidupan sehari-hari.

Secara umum kita perlu mengetahui jenis-jenis dari integral, seperti integral tentu dan tak tentu. Namun, perlu kita ketahui lebih dalam bahwa integral sendiri memiliki beragam jenisnya dan salah satunya adalah integral parsial. Jika dilihat maknanya secara umum, parsial berhubungan atau merupakan bagian dari sebuah keseluruhan. Dengan begitu, apabila kita memahami jenis integral parsial ini dengan baik tentunya akan memudahkan kita untuk mengerjakan soal-soal yang berhubungan dengan integral.

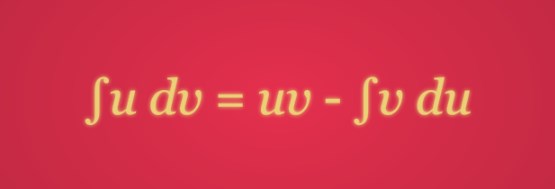
Baca juga: Rumus Integral, Jenis, dan Pembahasan

Baca juga: Rumus Integral Trigonometri dan Contoh Soal

Pada pembahasan kali ini, kalian akan mempelajari mengenai salah satu jenis integral, yaitu integral parsial mengenai makna, rumus, dan contoh soalnya. Berikut pembahasannya.

Pengertian Integral Parsial

Integral parsial merupakan salah satu bagian dari materi integral yang membahas mengenai cara menghitung integral dengan cara parsial. Teknik parsial sendiri merupakan teknik penyelesaian dengan cara memberikan pemisalan berdasarkan komponen yang diintegralkan. Biasanya, terdapat pemuatan variabel yang sama namun berbeda fungsinya. Penggunaan integral parsial biasanya dapat digunakan untuk menyelesaikan persamaan yang cukup kompleks.

Metode parsial dalam penyelesaian persoalan integral dapat digunakan apabila cara-cara lain tidak dapat digunakan untuk menyelesaikan sebuah soal integral, seperti sudah menggunakan integral subtitusi tetapi masih belum dapat ditemukan hasilnya. Meskipun prosesnya panjang, pada penerapan metode parsial dapat memudahkan kita untuk menyelesaikan soal integral yang rumit.

Biasanya, integral parsial menjadi satu-satunya kunci penyelesaian masalah integral apabila cara-cara lain tidak dapat diterapkan. Dengan begitu, pemahaman mengenai metode parsial ini perlu diterapkan lebih dalam agar dapat memahami masalah-masalah integral.

Bentuk umum sebuah integral parsial dapat ditunjukkan sebagai berikut.

Keterangan:

u = f(x), sehingga du = f(x)dx

dv = g(x)dx, sehingga v = g(x)dx

Jika f(x) berupa polinom derajat n ≥ 1, n ∈ asli menjadikan bentuk formula di atas bisa disederhanakan dengan tabel berikut.

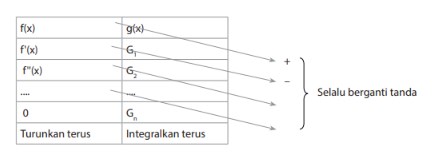
Berdasarkan tabel di atas, dapat kita lihat bahwa kolom fungsi f(x) di sebelah kiri merupakan fungsi yang harus diturunkan sampai turunannya bernilai 0. Lalu, pada kolom fungsi g(x) sebelah kanan harus diintegralkan sampai kolom sebelah kiri bernilai 0. Ketentuan lainnya adalah tanda fungsinya selalu beselang-seling, yaitu dari positif (+) menjadi negatif (–) dan seterusnya.

Baca juga: Rumus Integral Tertentu dan Tak Tentu

Rumus Integral Parsial

Dalam menerapkan metode parsial, perlu melakukan beberapa hal dasar agar memudahkan proses penyelesaiannya. Hal yang perlu diterapkan di awal adalah dengan menentukan suatu fungsi ke dalam rumusnya dengan menyamakan fungsi yang ada sesuai dengan tempat peletakan pada rumus integral parsial.

Rumus integral parsial dapat kita pahami seperti berikut.