Pengurangan dan Penjumlahan Vektor Beserta Contoh Soal – Jika berbicara mengenai pengurangan dan penjumlahan, tentunya hal yang terlintas adalah operasi hitung dasar matematika. Tentunya, pada operasi ini kita akan diperkenalkan dengan simbol-simbolnya agar dapat mengetahui makna dari operasi hitung yang dimaksud. Penjumlahan dan pengurangan dalam matematika dapat disimbolkan dengan tanda + dan -. Tanda + (plus) dibaca “ditambah” dan tanda – (minus) dibaca “dikurang”. Simbol tanda akan digunakan dalam sebuah kalimat matematika yang memiliki maksud untuk memecahkan sebuah penyelesaian matematika.
Sebagai sebuah operasi dasar, pengurangan dan penjumlahan dapat diterapkan dalam konsep matematika apa saja, termasuk pembahasan materi vektor. Vektor dalam konsep matematika dapat diartikan sebagai objek geometri yang memiliki besar dan arah, serta ditandai dengan tanda panah. Vektor yang dinyatakan dalam susunan urutan bilangan real memiliki operasi penjumlahan dan pengurangan yang sedikit berbeda dari operasi penjumlahan dan pengurangan aljabar biasa. Kondisi ini dikarenakan arah vektor mempengaruhi hasil penjumlahan/pengurangan vektor.
Baca juga: Perkalian Vektor Matematika dan Contoh Soal
Vektor dapat diartikan sebagai ruas garis berarah yang memiliki nilai panjang dan arah. Besaran vektor merupakan jenis besaran yang memiliki nilai dan arah. Contoh besaran vektor adalah perpindahan, kecepatan, percepatan, dan besaran lain yang memiliki nilai serta arah. Panjang vektor v merupakan jarak dari titik pangkal ke titik ujung dan ditulis dalam simbol |v|. Sebuah besaran vektor dapat dinyatakan dengan huruf kapital dengan cetak tebal seperti A atau dapat juga ditulis dengan sebuah huruf dan tanda panah pada bagian atas huruf.

Dalam operasi pengurangan dan penjumlahan pada konsep vektor sendiri akan ditampilkan beberapa metode yang dapat memudahkan kita untuk menghitungnya. Umumnya, beberapa metode penghitungan vektor dalam hal operasi pengurangan dan penjumlahan yang akan dibahas pada materi berikut.
Baca juga: Materi Rumus Matriks Matematika SMA
Pada pembahasan kali ini, kalian akan mempelajari mengenai operasi yang dapat diterapkan dengan metode vektor yaitu operasi pengurangan dan penjumlahan. Berikut pembahasannya.
Penjumlahan Vektor
Penjumlahan dua vektor dapat dilakukan secara geometri karena berhubungan dengan sebuah bidang. Operasi hitung penjumlahan dapat dilakukan pada dua buah vektor atau lebih. Cara melakukan operasi penjumlahan vektor dapat dilakukan dengan beberapa metode. Hal ini meliputi aturan segitiga dan aturan jajar genjang sebagai berikut.
1. Penjumlahan vektor dengan aturan segitiga
Penjumlahan dua buah vektor a dan b dapat dilakukan dengan arah yang berbeda sehingga dapat menggunakan aturan segitiga. Pada metode ini, dapat dilakukan dengan menggabungkan ujung vektor a dengan pangkal vektor b seperti pada gambar berikut.
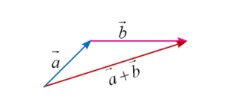
Pada penjumlahan di atas, dapat dilakukan berdasarkan resultan kedua vektor yang berarti jarak antara pangkal vektor a dan ujung vekto b. Dua buah vektor di atas dapat dijumlahkan dengan membentuk segitiga sehingga metode ini dapat dikatakan sebagai metode segitiga.
2. Penjumlahan vektor dengan aturan jajar genjang
Penjumlahan dua buah vektor dapat dilakukan dengan aturan jajar genjang yang melibatkan dua vektor yang telah diketahui dan adanya resultan vektor. Penjumlahan vektor a dan b dengan aturan jajar genjang dapat dilakukan dengan menggabungkan kedua ujung vektor. Pada penjumlahan vektor jajar genjang dapat dilakukan dari diagonal dengan ujung kedua vektor yang berpotongan dengan proyeksi ujung kedua vektor.
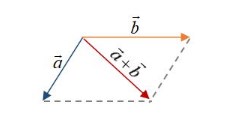
Dari gambar di atas, terdapat dua vektor a dan vektor b dengan resultan dari kedua vektor adalah a + b. Hal ini dapat dilihat ketiga vektor di atas dapat dijumlahkan dengan membentuk aturan jajar genjang. Hal ini dapat dilihat dari dua buah ruas garis yang masing-masing sejajar dengan kedua vektor sehingga saling berpotongan membentuk bangun jajar genjang.
3. Penjumlahan vektor dengan aturan poligon
Penjumlahan vektor berdasarkan geometri juga dapat diterapkan dengan metode poligon. Metode poligon adalah metode penjumlahan dua vektor atau lebih yang dilakukan dengan menempatkan pangkal vektor kedua pada ujung vektor pertama. Setelah itu, dapat menempatkan pangkal vektor ketiga di ujung vektor kedua hingga seterusnya.
Dalam metode poligon, dapat kita lihat resultan dari penjumlahan vektor terdapat pada vektor yang berpangkal di pangkal vektor pertama dan berujung di ujung vektor akhir. Misalnya, dapat kita lihat pada vektor metode poligon berikut.
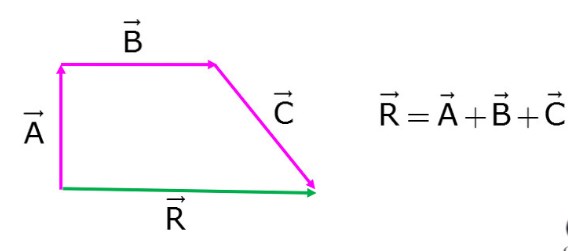
4. Metode Analitis
Penjumlahan vektor dapat dilakukan dengan metode analitis yang dapat menjumlahkan dua buah vektor tanpa menggambar vektor terlebih dahulu. Penjumlahan dengan metode analitis bertujuan untuk menguraikan vektor pada sumbu melalui proyeksi. Hasil proyeksi ini akan berupa komponen vektor yang terletak pada sumbu suatu bidang.
Misalnya, sebuah vektor terletak pada bidang kartesius pada R2. Proyeksi vektor akan menghasilkan komponen vektor pasa sumbu x dan sumbu y. Nilai komponen vektor F pada sumbu X adalah Fx = F·cos α, sedangkan nilai komponen F pada sumbu Y adalah Fy = F·sin α. α merupakan sudut yang dibentuk suatu vektor dengan sumbu X. Resultan vektor pada penjumlahan dengan metode analisis dapat dihitung dengan persamaan FR2 = ∑Fx2 + ∑Fy2. FR adalah resultan/hasil penjumlahan vektor, Fx adalah komponen vektor pada sumbu x, dan Fy adalah komponen vektor pada sumbu y.
Baca juga: Rumus Integral, Jenis, dan Pembahasan
Rumus Penjumlahan Vektor
Penjumlahan vektor dapat dilakukan dengan dua buah vektor pada dimensi 2 yang dinyatakan dalam vektor arah a = (x1 dan y1) dan vektor b = (x2 dan y2) dengan begitu arah vektor penjumlahan dapat dinyatakan dengan persamaan vektor arah (a + b) = (x1 + y1 . x2 + y2). Dengan begitu, dapat kita simpulkan rumus penjumlahan kedua vektor sebagai berikut.

Pengurangan Vektor
Pengurangan pada dasarnya adalah kebalikan dari penjumlahan. Pengurangan dua buah vektor dapat menggunakan penerapan seperti metode penjumlahan, yaitu metode segitiga dan jajar genjang. Bedanya, cara pengurangan dua buah vektor dapat dilakukan dengan membuat arah vektor menjadi berkebalikan. Berikut contohnya.
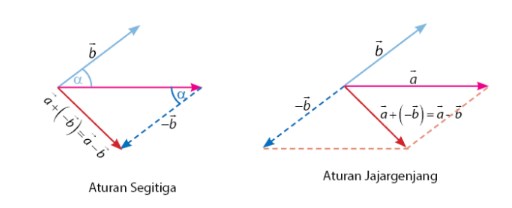
Rumus Pengurangan Vektor
Pengurangan dalam dua buah vektor pada dimensi 2 dapat dinyatakan dalam vektor arah a = (x1, y1) dan vektor b = (x2, y2) dengan begitu vektor untuk penjumlahan dua vektor dinyatakan dengan persamaan vektor arah (a + b) = (x1 – x2, y1 – y2). Dengan begitu, dapat kita simpulkan rumus pengurangan kedua vektor sebagai berikut.

Sifat Penjumlahan dan Pengurangan Vektor
Penjumlahan dan pengurangan pada sebuah vektor memiliki beberapa sifat sehingga dapat dijadikan patokan atau hukum penghitungannya. Dalam penjumlahan vektor, dapat kita pahami bahwa operasi hitung ini memiliki sifat komutatif dan asosiatif. Komutatif sendiri merupakan sifat yang dapat digunakan untuk menukar angka dan jawabannya sehingga hasilnya tetap sama, sedangkan asosiatif merupakan cara pengelompokkan operasi bilangan dengan urutan berbeda.
Berbeda dengan penjumlahan, operasi pengurangan vektor memiliki sifat atau prinsip yang berkebalikan. Meskipun cara kerjanya sama, pada pengurangan vektor perlu membalik arah vektor pengurangannya. Misalnya, terdapat pengurangan dua buah vektor A dan B, maka vektor A dikurangi vektor B sama dengan vektor A ditambah negatif vektor B. Negatif vektor B dapat diperoleh dengan membalik vektor B ke arah yang berlawanan, sehingga pengurangan vektor A oleh vektor B.





