Perkalian Vektor Matematika dan Contoh Soal – Dalam ilmu matematika, terdapat berbagai konsep perkalian yang banyak diterapkan dalam sebuah perhitungan. Salah satunya adalah pembahasan mengenai perkalian vektor yang membahas mengenai dua objek yang akan dikalikan. Pada perkalian vektor sendiri, nantinya kita akan dikenalkan dengan adanya dua jenis besaran pada perhitungannya.
Dalam menyelesaikan perkalian pada vektor dapat dituntaskan berdasarkan pola-polanya. Hal ini tentunya akan memberikan kemudahan kita dengan cara memahami sifat-sifat perkaliannya. Vektor sendiri dapat diartikan sebagai perkalian dengan besaran yang mempunyai nilai dan arah. Konsep vektor ini dapat kita gunakan dalam kehidupan sehari-hari yang dapat diterapkan penggunaannya dalam bidang fisika, teknik, komputer, hingga desain grafis. Penggunaan vektor dalam perkalian dapat kita ketahui berdasarkan rumus perkalian hingga sifat perkaliannya. Selain itu, agar lebih mengetahui perkalian vektor dapat kita pahami macam-macamnya yang dapat diklasifikan dengan adanya jenis perkalian skalar dengan vektor, vektor dengan vektor, dan vektor dengan yang lainnya.
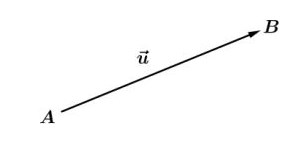
Pemahaman mengenai vektor dapat kita dapatkan dengan pemahaman fisika yang melambangkan besar vektor dengan adanya garis pada anak panah. Anak panah pada lambang melambangkan vektornya yang dapat bertransformasi. Pada gambar di bawah ini, kalian dapat melihat transformasi titik A pada vektor u dengan menghasilkan titik B. Hal ini dapat dimaknai bahwa vektor u dapat menjadi garis berarah dari titik A ke titik B.
Baca juga: Pengurangan dan Penjumlahan Vektor Beserta Contoh Soal
Pada pembahasan kali ini, kalian akan mempelajari mengenai perkalian vektor dengan macam-macamnya yang disertai rumus dan contoh soalnya. Berikut pembahasannya.
Pengertian Vektor
Perkalian vektor dapat dimaknai sebagai operasi perkalian dengan dua operand (objek yang dikalikan) berupa vektor dan dapat tidak vektor. Dalam perkalian vektor, biasanya tidak hanya meliputi operasi pengurangan maupun penjumlahan vektor saja dengan beberapa kategorinya.
Notasi pada perkalian vektor umumnya dapat kita lihat seperti berikut.
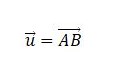
Pada vektor AB pada contoh di atas, dapat kita ketahui bahwa pangkal vektor yang terletak pada titik A dan ujung vektor yang terletak pada titik B. Berkaitan dengan kesamaan dua vektor, dua vektor dapat dikatakan sebagai vektor yang sama jika nilai (panjang vektor) dan arahnya sama.

Baca juga: Pengertian, Rumus Dan Contoh Soal Translasi
Umumnya, terdapat tiga macam perkalian vektor, yaitu produk skalar, perkalian silang, dan perkalian langsung.
1. Produk skalar
Pada perkalian vektor, produk skalar dapat ditandai dengan adanya dua buah vektor yang akan menghasilkan sebuah skalar. Pada perkalian ini dapat bersifat komutatif seperti berikut.
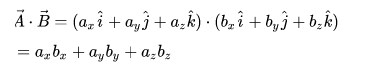
Pada vektor satuan akan dilihan hubungan-hubungan yang khusus dalam perkalian ini dan dapat dijadikan sebagai sifat-sifatnya sebagai berikut.

2. Perkalian silang
Perkalian silang pada dua buah vektor akan dapat menghasilkan sebuah vektor. Dalam perkalian silang tidak memiliki sifat komutatif. Berikut contohnya.

3. Perkalian langsung
Perkalian langsung pada dua buah vektor dapat berupa tensor atau matriks. Dalam perkalian langsung ini tidak memiliki sifat komutatif. Berikut contohnya.

Baca juga: Materi Rumus Matriks Matematika SMA
Operasi Perkalian Vektor
Berdasarkan macam-macam dari perkalian vektor, berikut akan kita bahas operasi perkalianya yang akan disesuaikan dengan rumus dan sifat-sifatnya.
1. Perkalian vektor dengan skalar
Perkalian vektor dengan skalar merupakan perkalian yang meliputi perpindahan pada sebuah benda. Misalnya Ani mengendarai kendaraan beroda empat menuju arah barat dengan kecepatan 40 km/jam. Kemudian terjadi perpindahan antara Ani dengan kendaraan beroda empat sesudah beberapa waktu. Umumnya, akan kita gunakan rumus s = v x t.
Rumus kecepatan ini dapat kita terapkan perpindahan jenis besaran skalar dan vektornya. Pada kategori besaran skalar ialah waktu, sedangkan untuk kategori besaran vektor ialah kecepatan. Maka dari itu perkalian antara waktu dengan kecepatan tersebut membuat perpindahan yang pada alhasil menghasilkan besaran vektor. Dengan begitu, dapat disimpulkan bahwa perkalian vektor dengan skalar akan menghasilkan vektor.
Rumus sederhana perkalian vektor dengan skalar dapat kita lihat seperti berikut.
B = k x A
Keterangan:
B = vektor B
k = skalar
A = vektor A
Pada rumus di atas dapat diterapkan juga pada pemberlakukan perkalian vektor satuan dengan skalar, baik untuk tiga dimensi maupun dua dimensi. Jika dijabarkan lebih lanjut maka rumus perkalian antara vektor satuan dengan skalar akan menjadi menyerupai di bawah ini.






