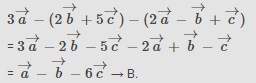Pengurangan dan Penjumlahan Vektor Beserta Contoh Soal

Agar mempermudah pemahaman kalian, pahami sifat penjumlahan dan pengurangan vektor pada tabel berikut.

Baca juga: Pertidaksamaan Logaritma dan Contoh Soal

Contoh Soal

Setelah mempelajari mengenai vektor pada operasi hitung pengurangan dan penjumlahannya berdasarkan rumus dan hukumnya, kalian dapat memahaminya lebih dalam dengan membahas soal-soal berikut ini.

1. Diketahui 3 vektor yang dinyatakan dengan persamaan a = 3i – 2j, b = –i + 4j, dan c = 7i – 8j. Jika vektor r dinyatakan dalam persamaan vektor r = k·a + m·b maka nilai k + m adalah ….

Pembahasan:

Menentukan persamaan vektor:

r = k·a + m·b
7i – 8j = k(3i – 2j) + m(–i + 4j)
7i – 8j = 3ik – 2jk – im + 4jm
7i – 8j = 3ik – im – 2jk + 4jm
7i – 8j = (3k – m)i + (–2k + 4m)j

Berdasarkan persamaan di atas dapat diperoleh dua persamaan yaitu,

• 3k – m = 7
• 2k – 4j = 8

Selanjutnya, kita dapat menentukan nilai k dan m berdasarkan dua persamaan di atas.

Mencari nilai k:

Diperoleh nilai k = 2 dan m = -1. Jadi, k + m = 2 + (-1) = 1.

 

2. Hitunglah bentuk sederhana dari

Pembahasan: