Contoh Soal Kongruen Dan Kesebangunan

Contoh Soal Kongruen Dan Kesebangunan – Sebagian orang, pasti pernah mengukur dan membandingkan sebuah benda satu ke benda lainnya. Misalnya, jika kalian melihat kunci kamar dan kunci gerbang pasti memiliki bentuk yang berbeda-beda. Apabila kunci hilang, kalian perlu membuat duplikat kunci tersebut dan tidak dapat menggunakan kunci lain. Hal ini lah yang dinamakan kongruen sebuah benda.

Selain kongruen, sebuah benda dapat dikatakan kesebangunan. Misalnya, jika kalian melihat sebuah peta pasti terdapat skala yang menjelaskan perbandingan. Perbandingan ini melambangkan ukuran sebenarnya suatu daerah dengan yang digambar. Dalam dunia matematika, hal ini dikenal dengan istilah kesebangunan.

Kali ini, kalian akan mempelajari lebih lanjut mengenai materi matematika satu ini. Tak lupa, untuk lebih mengasah pemahaman kalian akan dihadirkan beberapa contoh soal yang dapat digunakan sebagai latihan. Berikut penjelasannya.

Baca juga: Rumus Kesebangunan Bangun Datar

Kesebangunan

Kesebangunan biasanya terjadi pada dua buah bangun datar yang dapat dinyatakan sebangun. Sebangun memiliki makna apabila terdapat kesesuaian sama besar di antara sisi-sisi sebanding pada sebuah bangun.

Kesebangunan pada sebuah bangun datar dapat dilambangkan dengan notasi ~. Biasanya, prinsip kesebangunan dapat dimanfaatkan dalam perbesaran sebuah foto dan pembuatan model benda. Namun, perlu diingat bahwa materi kesebangunan merupakan materi penerus dari materi dilatasi. Materi dilatasi membahas mengenai proses memperbesar dan memperkecil bangun datar, sedangkan materi kesebangunan mempelajari bagaimana mengukur dan membandingkan ukuran bangun datar.

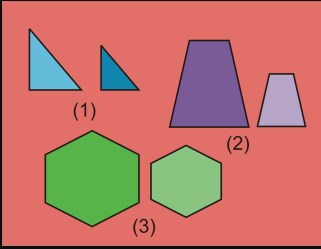
Setiap bangun datar yang sebangun memiliki beberapa sifat-sifat yang harus dimilikinya. Hal ini akan memudahkan pemahaman kalian dalam memilah bangun datar terkait. Berikut penjelasannya.

Dua bangun datar yang sebangun

Dua bangunan datar yang memiliki korespondensi satu-satu antar titik-titik sudutnya dapat dikatakan sebangun apabila sudutnya berkorespondensi sama besar dan semua perbandingan panjang sisi-sisinya bersesuaian.

Dengan begitu, terdapat sifat-sifat yang dimiliki dua bangun datar yang sebangun sebagai berikut.

1. Perbandingan yang sama panjang di kedua sisinya.
2. Besaran sudut yang sama di setiap titiknya.

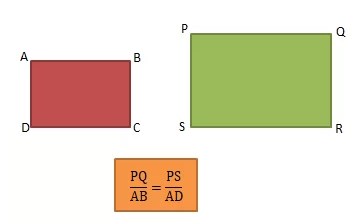
Berikut merupakan contoh rumus bangun datar sebangun berbentuk persegi.

Baca juga: Sifat Sifat Tabung Dan Gambar Jaring Jaring

Dua segitiga yang sebangun

Berikut sifat-sifat yang dimiliki dua buah segitiga yang sebangun.

1. Sisi-sisi yang bersesuaian memiliki perbandingan panjang sama.
2. Besar sudut yang bersesuaian sama besar.
3. Sudut-sudut yang bersesuaian memiliki perbandingan yang sama sehingga sudut yang diapit pada kedua sisinya memiliki besar yang sama.

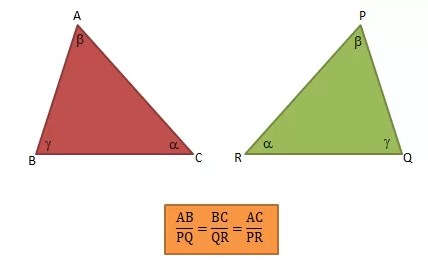
Berikut merupakan contoh rumus bangun datar sebangun berbentuk segitiga.

Segitiga istimewa yang sebangun

Segitiga merupakan salah satu bangun datar yang memiliki beberapa bentuk. Setiap bentuk memiliki sifat yang berbeda-beda untuk dikatakan sebangun dan diuraikan sebagai berikut.

1. Segitiga siku-siku harus memiliki sudut yang salah satunya memiliki besar 90⁰.
2. Segitiga sama kaki harus memiliki dua sisi yang sama panjang, dua sudut sama besar, dan satu sumbu simetri pada bangunnya.
3. Segitiga sama sisi harus memiliki sifat panjang di setiap ketiga sisinya, tiga buah sudut yang sama besar, dan tiga sumbu simetri.

Berikut salah satu contoh rumus segitiga siku-siku yang memiliki keistimewaan sebagai berikut.

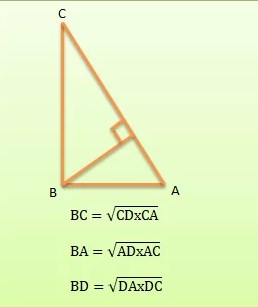
Baca juga: Rumus Luas Permukaan Kubus Dan Volume Kubus

Kekongruenan

Definisi dari kekongruenan sebuah bangunan masih terkait dengan kesebangunan. Hal ini karena dalam kongruen merupakan kasus khusus sebuah kesebangunan. Dua buah bangunan dapat dikatakan kongruen apabila memiliki korespondensi satu-satu antara titik-titik sudut.

Kekongruenan sebuah bangun datar dapat dilambangkan dengan simbol notasi ≅. Biasanya, kekongruenan memiliki keberlakuan, yaitu sudut pada bangunan memiliki besar yang sama besar dan memiliki perbandingan panjang sisi yang bersesuaian adalah satu.

Beberapa bangun datar yang kongruen memiliki sifat-sifat berikut.

1. Bentuk yang sama dari kedua bangun.
2. Sisi-sisi dari bangun memiliki panjang yang sama besar.
3. Biasanya berbentuk dua bangun persegi dan persegi panjang.

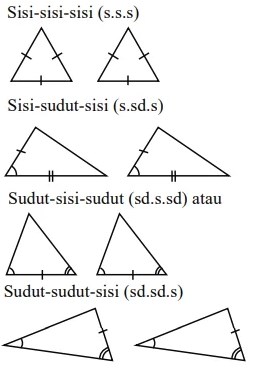
Kemudian, pada bangun datar yang berupa segitiga memiliki sifat kongruen berikut.

1. Sisi yang bersesuaian memiliki ukuran yang sama besar (sisi-sisi-sisi).
2. Dua sisi yang bersesuaian memiliki besar yang sama dan diapit oleh kedua sisi yang sama besar (sisi-sudut-sisi).
3. Satu sisi yang mengapit dan dua sudut yang saling bersesuaian sama besar (sudut-sisi-sudut).

Baca juga: Contoh Rumus ABC Persamaan Kuadrat

Contoh Soal

Selanjutnya, setelah mempelajari materi kongruen dan kesebangunan sekilas saatnya kalian mengasah kemampuan terkait materi tersebut. Setiap contoh soal akan disertai pembahasan yang diharapkan dapat lebih jelas dalam mempelajari materi kongruen dan kesebangunan. Selamat mengerjakan!

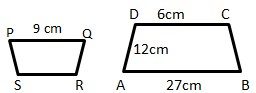
1. Berikut merupakan dua buah bangun datar berbentuk trapesium.