Perkalian Matriks Dan Contoh Soal Lengkap

Cara Perkalian Matriks –  Perkalian matriks adalah salah satu pelajaran penting yang ada dalam ilmu matematika. Pengertian matriks adalah sekumpulan bilangan yang susunannya terdiri dari baris maupun kolom. Atau bisa pula merupakan susunan dari keduanya. Untuk kumpulan bilangan ini umumnya diapit dengan menggunakan tanda kurung.

Untuk bilangan-bilangan yang telah disusun pada matriks ini biasa disebut sebagai elemen-elemen matriks.  Sedangkan ukuran matriks biasa disebut sebagai ordo matriks. Misalnya saja matriks dengan ordo 3 x 2, maka berarti matriks tersebut memiliki 3 baris dan 2 kolom.

Matriks sendiri memiliki banyak sekali macam jenisnya. Beberapa diantaranya adalah matriks kolom, matriks baris, matriks persegi, matriks persegi panjang, matriks diagonal, matriks segitiga, dan jenis matriks yang lainnya.

Pengertian Perkalian Matriks

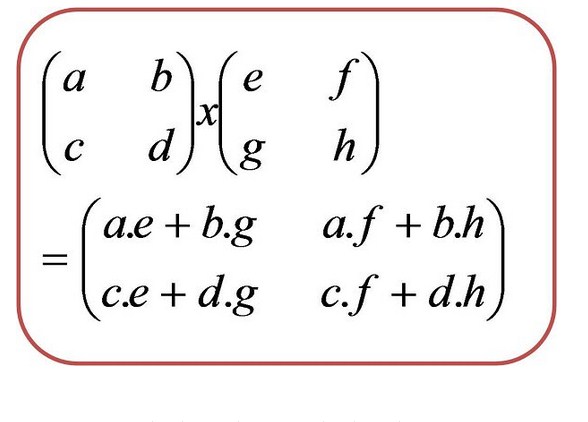
Pengertian dari perkalian matriks adalah sebuah nilai matriks yang bisa dihasilkan dengan cara masing-masing barisnya dikalikan dengan setiap kolom, dimana jumlah pada barisnya sama. Untuk setiap anggota elemen matriks selanjutnya akan dikalikan dengan anggota elemen matriks yang lainnya.

Adapun hal tersebut harus dilakukan sesuai dengan urutan dan aturan yang sudah ditentukan dalam perkalian bilangan matriks. Pada saat Anda melakukan perhitungan nilai matriks maka Anda bisa melihat adanya suatu kolom dan baris. Keduanya biasa digunakan untuk dapat menentukan serta menghitung nilai matriks. Kolom dan baris memang sangat dibutuhkan dalam melakukan perhitungan nilai matriks.

Perlu Anda ketahui bahwa rumus matematika matriks ini sebenarnya merupakan suatu turunan yang diperoleh langsung dari operasi dasar matriks. Hal tersebut karena jenis matriks matematika berdasarkan operasi pada umumnya dibagi menjadi rumus penjumlahan matriks, rumus pengurangan matriks, rumus perkalian skalar matriks, rumus pengurangan matriks, dan juga rumus mencari perkalian matriks.

Baca Juga: Rumus Matriks Invers

Sifat-Sifat Perkalian Matriks

Perkalian matriks ternyata juga memiliki beberapa sifat yang tertentu. Adapun sifat-sifat perkalian matriks adalah sebagai berikut ini:

• Sifat matriks komutatif terhadap penjumahan, yaitu A + B = B + A
• Sifat matriks assosiatif terhadap penjumlahan, yaitu (A + B) + C = A + ( B + C)
• Sifat matriks matriks nol, yaitu A + 0 = A
• Sifat matriks lawan matriks, yaitu A + (-A) = 0
• Sifat matriks asoasiatif terhadap perkalian, yaitu (AB) C = A (BC)
• Sifat matriks distributif kiri, yaitu A(B + C) = AB + AC
• Sifat matriks distributif kanan : (A+B) C = AC + BC
• Sifat matriks perkalian dengan konstanta , yaitu  k(AB) = (kA)B = A (kB), yang dimana k konstanta real
• Sifat matriks  perkalian dengan matriks satuan, yaitu AI = IA = A

Jenis-Jenis Perkalian Matriks

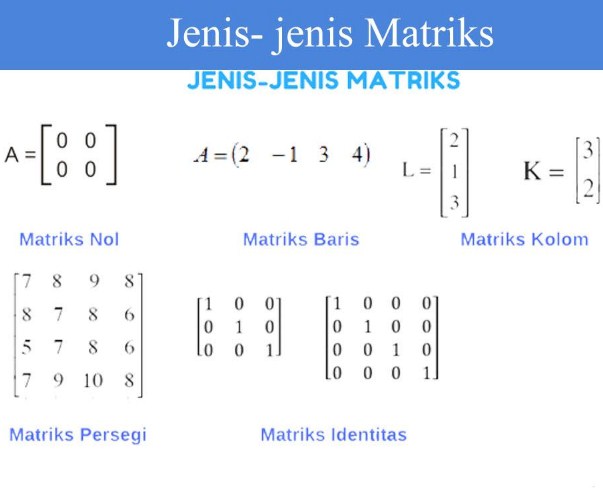
Perkalian matriks juga memiliki beberapa macam, berikut ini adalah jenis-jenis perkalian matriks yang perlu Anda ketahui:

1. Matriks Baris

Matriks baris merupakan salah satu jenis matriks yang hanya memiliki satu baris saja. Ordo dari matriks baris pada umumnya memiliki bentuk 1 x  n yang dimana n dapat menentukan banyaknya kolom dari matriks baris tersebut.