Contoh Soal Dan Rumus Matriks Invers

Rumus Matriks Invers – Selamat datang di website kami. Pada kesempatan kali ini kami akan membahas invers matrik secara lengkap mulai dari pengertian matriks, pengertian invers matriks, jenis-jenis, sifat beserta rumus dan contoh soalnya. Dengan adanya pembahasan yang akan kami jabarkan secara lengkap ini kami harapkan pembaca bisa memahaminya dengan mudah.

Invers suatu matriks banyak dijadikan sebagai pertanyaan dalam sebuah soal matriks. Bahkan juga sering muncul dalam beberapa soal matriks. Maka dari itu, sudah seharusnya Anda menguasai bagaiamana cara mencari matrik inverse terutama Anda yang masih pelajar. Soal-soal seperti ini akan kita temui di pelajaran SMA dan juga perkuliahan.

Invers matriks sendiri terdiri dari beberapa macam, salah satunya adalah invers matriks 2×2 dan 3×3. Cara menghitungnya pun sudah pasti berbeda-beda, namun untuk cara perhitungan matrik 2×2 akan jauh lebih mudah jika dibandingkan dengan lainnya. Untuk lebih jelasnya mari langsung saja simak pembahasan selengkapnya di bawah ini.

Pengertian Matriks

Matriks merupakan suatu kumpulan bilang yang bisa disusun dengan baris atau secara kolom atau bisa pula disusun oleh kedua-duanya serta diapit dalam tanda kurung (). Bagian-bagian matriks terdiri dari beberapa bilangan tertentu yang telah membentuk di dalam sebuah matriks.

Matris sendiri pada umumnya banyak digunakan sebagai penyederhana dalam penyampaian data. Dengan demikian maka akan jauh lebih mudah lagi untuk diolah lebih lanjutnya.

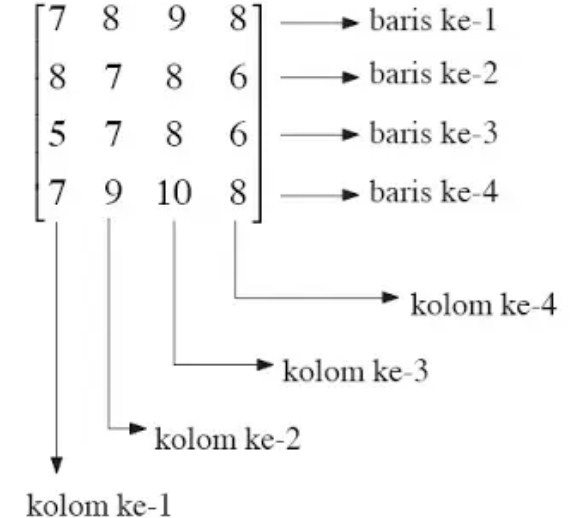
Sama halnya dengan variabel, matriks juga bisa dimanipulasi seperti dijumlahkan, dikalikan, dikurangkan dan didekomposisikan. Dengan adanya representasi matriks tentunya perhitungannya bisa dilakukan secara lebih struktur.

Pengertian Invers Matriks

Lalu apa yang dimaksud dengan invers Matriks? Sebelumnya perlu diketahui bahwa invers suatu matriks umumnya akan digambarkan dengan nama matriks yang tertentu (dalam bentuk huruf kapital) dan dipangkatkan -1. Untuk lebih jelasnya kami akan memberikan sebuah contoh yang dimana matriksnya adalah matriks A, maka invers dari matriks A tersebut harus ditulis dengan A^-1 .

Sementara itu invers matriks dapat didefinisikan dimana jika A merupakan sebuah matriks kuadrat, maka Anda dapat mencari matriks B dengan cara AB = BA – 1. A dikatakan dapat dibalik atau invertible sedangkan untuk B disebut sebagai invers dari A.

Setelah memahami mengenai pengertian matriks dan pengertian invers matrik, maka selanjutnya Anda harus paham bagaimana cara menyelesaikan soal yang berkaitan dengan invers matriks. Namun sebelum menuju ke rumus dan contoh soal kami juga akan menjelaskan mengenai macam-macam matriks terlebih dahulu untuk melengkapi pembahasan kali.

Baca Juga: Cara Perkalian Matriks Dan Contoh Soal

Macam-Macam Matriks

Matriks ternyata memiliki banyak sekali macam jenisnya. Berikut ini adalah beberapa macam matriks yang perlu Anda ketahui:

1. Matriks Baris

Matriks baris adalah sebuah matriks yang hanya terdiri dalam satu baris.

Contoh Matriks Baris :

P = [3 2 1]

Q = [4 5 – 2 5]