Rumus Fungsi Invers – Saat belajar matematika Anda tentunya sering menjumpai lebih dari satu fungsi matematika. Memang ada banyak sekali fungsi dalam pelajaran matematika. Dari sekian banyaknya fungsi pada matematika, yang paling menarik untuk dipelajari adalah fungsi komposisi dan juga fungsi invers.
Nah, pada pembahasan kali ini kami akan mengulas tentang fungsi komposisi dan fungsi invers mulai dari pengertian, rumus, sifat-sifat, hingga fungsi keduanya dalam kehidupan. Untuk lebih jelasnya mari langsung saja kita simak pembahasan selengkapnya di bawah ini.

Pengertian Fungsi Komposisi
Apa itu fungsi komposisi? Pengertian dari Fungsi komposisi adalah suatu penggabungan dari operasi dua jenis fungsi f(x) dan g(x) sehingga nantinya dapat menghasilkan fungsi yang baru.
Rumus Fungsi Komposisi
Operasi untuk fungsi komposisi ini pada umumnya dilambangkan dengan huruf atau simbol “o”. Lambang tersebut bisa dibaca komposisi atau bisa juga bundaran. Fungsi baru inilah yang bisa terbentuk dari f(x) dan juga g(x) yakni:
- (f o g)(x) artinya adalah g dimasukkan ke f
- (g o f) (x) artinya adalah f dimasukkan ke g
Fungsi tunggal merupakan salah satu fungsi yang dapat dilambangkan dengan huruf “f o g” atau bisa pula dibaca dengan “f bundaran g”. Selanjutnya untuk Fungsi ( f o g) (x) → f (g (x)) dapat dikomposisikan menjadi fungsi f (x).
Sementara itu, untuk “g o f” dapat dibaca sebagai fungsi g bundaran f. Sehingga “g o f” merupakan fungsi f yang harus diselesaikan terlebih dahulu dari fungsi g. Supaya memudahkan Anda dalam memahami mengenai materi fungsi ini, silahkan Anda perhatikan gambar berikut ini:
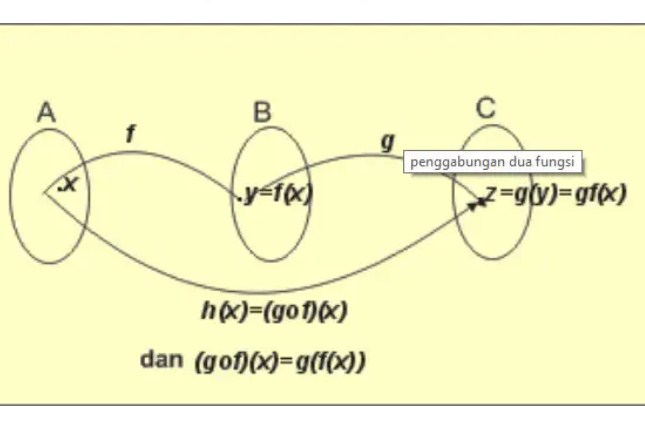
Dilihat dari skema rumus diatas maka bisa diketahui bahwa :
Apabila f : A → B maka ditentukan dengan menggunakan rumus y = f(x)
Apabila g : B → C maka ditentukan dengan menggunakan rumus y = g(x)
Jadi akan diperoleh suatu hasil fungsi g dan juga f, yaitu:
h(x) = (gof)(x) = g( f(x))
Dari definisi tersebut maka bisa kita ambil kesimpulan bahwa fungsi yang melibatkan antara fungsi f dengan g bisa ditulis seperti berikut ini:
- (g o f)(x) = g(f(x))
- (f o g)(x) = f(g(x))
Baca Juga: Rumus Invers Matriks
Sifat-Sifat Fungsi Komposisi

Ternyata ada banyak sekali sifat yang dimiliki oleh fungsi komposisi. Adapun sifat-sifat pada fungsi komposisi adalah sebagai berikut ini:
Apabila f : A → B , g : B → C , h : C → D, maka akan berlaku berbagai sifat seperti berikut ini:





