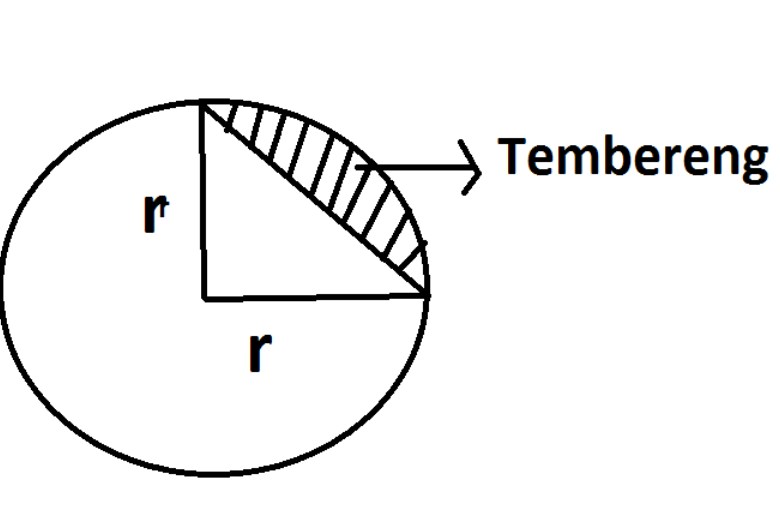
Luas Tembereng Lingkaran – Mungkin Anda sering mendengar istilah lingkaran. Lingkaran memiliki banyak sekali unsur di dalamnya. Salah satunya adalah tembereng lingkaran.
Nah, pada kesempatan kali ini kami akan membahas mengenai rumus tembereng lingkaran secara lengkap beserta contoh soalnya.
Namun sebelum itu simak terlebih dahulu mengenai penjelasan bangun datar lingkaran berikut ini.

Pengertian lingkaran dalam matematika adalah suatu bangun datar dengan dua dimensi. Lingkaran juga merupakan sekumpulan dari banyak titik yang telah membentuk sebuah lengkungan yang mempunyai panjang sama pada titik pusat lingkaran.
Lengkungan-lengkungan yang ada di dalam lingkaran akan saling berhubungan dan mengelilingan titik pusat serta membentuk di daerah di bagian dalamnya. Sebuah bangun lingkaran sudah pasti mempunyai luas dan keliling.
Adapun rumus yang digunakan untuk menghitung luas lingkaran adalah π × r². Sedangkan rumus untuk mencari keliling lingkaran yaitu 2 × π × r.
Unsur-Unsur Lingkaran Matematika

Seperti yang sudah kami jelaskan diatas bahwa sebuah lingkaran sudah pasti memiliki beberapa bagian atau unsur di dalamnya. Beberapa bagian tersebut meliputi jari-jari, diameter, juring, tembereng, dan lain sebagainya.
Pada dasarnya dalam sebuah lingkaran memiliki 10 unsur. Untuk memahami lebih lanjut mengenai unsur-unsur yang ada di dalam lingkaran, berikut ini kami akan memberikan penjelasan secara detail mengenai masing-masing unsur tersebut.
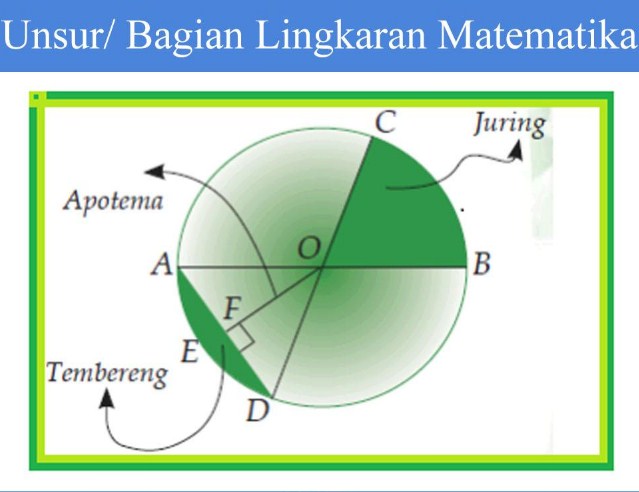
- Jari-Jari Lingkaran
Jari-jari lingkaran adalah sebuah garis yang berfungsi untuk menghubungkan antara satu titik pusat dengan titik pada bagian keliling lingkaran. Jari-jari dapat menentukan seberapa luaskah bidang lingkaran, karena jari-jari mempunyai informasi yang berupa jarak tetap dari titik pusat lingkaran untuk menuju kumpulan titik lengkung. Bagian jari-jari pada gambar lingkaran diatas berada pada garis OC, OD, OB dan OA.
- Titik Pusat Lingkaran
Sesuai dengan namanya, titik pusat adalah sebuah titik yang dimana letaknya berada tepat di bagian tengah-tengah lingkaran. Bagian titik inilah yang akan menjadi pusat terbentuknya garis lengkung lingkarang dengan berbagai macam ukuran. Bagian titik pusat lingkaran pada gambar lingkaran diatas berada pada huruf O.
- Busur Lingkaran
Busur lingkaran adalah sebuah garis lengkung yang juga merupakan bagian dari keliling lingkaran. Busur lingkaran terdiri dari dua macam, yaitu busur besar dan busur kecil. Busur lingkaran bisa disebut sebagai busur besar jika memiliki panjang yang lebih dari setengah lingkaran.
Sementara itu, busur lingkaran bisa disebut sebagai busur kecil jika memiliki panjang yang kurang dari setengah lingkaran. Bagian busur lingkaran pada gambar diatas berada pada garis lengkung AC, CB, BD, dan AD.