Rumus Persamaan Garis Lurus Dan Gradien

Persamaan Garis Lurus – Selamat datang diwebsite kami caraharian.com yang selalu uptodate dalam membahas pelajaran matematika. Nah, kali ini kami akan membahas salah satu materi matematika yang penting untuk dipelajari, yaitu persamaan garis lurus dan gradien.

Ulasan materi yang akan kami sampaikan kali ini meliputi gradien, rumus persamaan garis lurus, dan  metode cara untuk menentukan persamaan garis lurus. Untuk melengkapi materi ini pada bagian akhir kami juga akan memberikan contoh soal yang sudah dilengkapi dengan jawabannya sehingga akan memudahkan Anda untuk mempelajarinya.

Sebelumnya perlu diketahui bahwa ciri-ciri yang dimiliki oleh persamaan garis lurus adalah variebelnya memiliki pangkat tertinggi satu. Nah, sebelum Anda mempelajari materi ini untuk dapat menentukan persaman garis lurus, maka Anda harus memahami cara menggambar persamaan garis lurus. Hal ini karena materi tersebut akan sangat membantu Anda dalam memahami materi persamaan garis lurus.

Pengertian garis lurus sendiri adalah sekumpulan titik-titik yang memiliki jumlah tak terhingga dan saling berdampingan. Garis lurus dapat dinyatakan dalam berbagai macam bentuk persamaan garis lurus, bahkan sebuah garis lurus dapat dinyatakan dalam lebih dari satu persamaan.

Pengertian Persamaan Garis Lurus

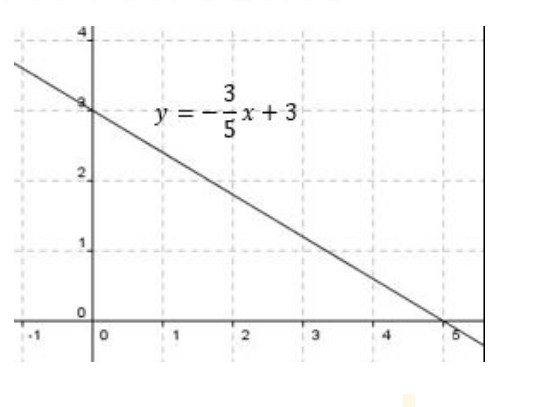
Seperti yang sudah kami jelaskan sebelumnya bahwa persamaan ini menyatakan suatu persamaan yang bisa mengartikan sebuah garis lurus ke dalam sebuah persamaan. Jadi, definisi dari persamaan garis lurus adalah suatu persamaan yang jika digambarkan ke dalam suatu bidang koordinat cartesius hasilnya akan membentuk suatu garis lurus. Adapun yang dimaksud garis lurus adalah sekumpulan titik-titik yang letaknya saling sejajar atau lurus.

Gradien

Sebelum membahas lebih lanjut mengenai rumusnya, penting sekali untuk mengetahui sebuah komponen yang tidak bisa lepas dari persamaan garis lurus. Adapun komponen penting yang kami maksud disini adalah gradien.

Gradien adalah sebuah perbandingan komponen y dan komponen x, atau yang biasa disebut dengan kecondongan dari sebuah garis. Lambang atau simbol yang dimiliki oleh gradien adalah huruf m.

Gradien juga dapat diartikan sebagai suatu nilai yang telah menyatakan kemiringan suatu garis. Pada umumnya, nilai dari gradien pada sebuah persamaan garis lurus akan dinyatakan melalui perbandingan yaitu i Δy/Δx..

Untuk lebih jelasnya silahkan Anda perhatikan cara untuk dapat menentukan gradien pada gambar berikut ini:

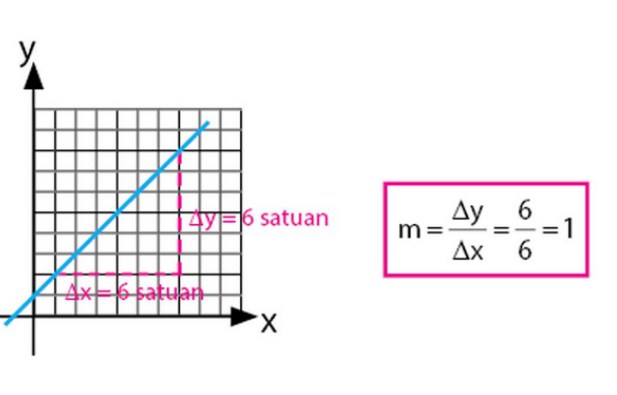
Cara untuk dapat menentukan suatu gradien pada suatu garis lurus dalam bidang kartesius juga dapat dipengaruhi oleh arah kemiringan garis itu sendiri. Silahkan simak lebih lanjut mengenai cara menentukan gradien garis pada ulasan berikut ini:

1. Gradien dari persamaan ax + by + c = 0
   M = yaitu komponen X atau komponen Y
2. Gradien yang telah melalui titik pusatnya ( 0, 0 ) dan juga titik ( a, b )
   m = b / a
3. Gradien yang telah melalui titik nya  ( x₁, y₁) dan juga ( x₂, y₂)
   m = y₁ – y₂ / x₁ – x₂ atau m = y₂ – y₁ / x₂ – x₁
4. Gradien yang garis nya saling sejajar  ( / / )
   m = sama atau jika misalnya di simbolkan akan menjadi m₁= m₂
5. Gradien pada garis nya yang saling tegak lurus atau lawan dan kebalikan
   m = -1 maupun  m₁x m₂= -1

Baca Juga: Sistem Persamaan Linear Dua Variabel

Posisi Antara 2 Garis

Posisi antara 2 buah garis yang ada pada persamaan garis lurus dapat dibedakan menjadi dua macam jenis, yaitu saling sejajar dan tegak lurus. Kedua posisi ini ternyata memiliki persamaan garis lurus yang saling berkaitan.

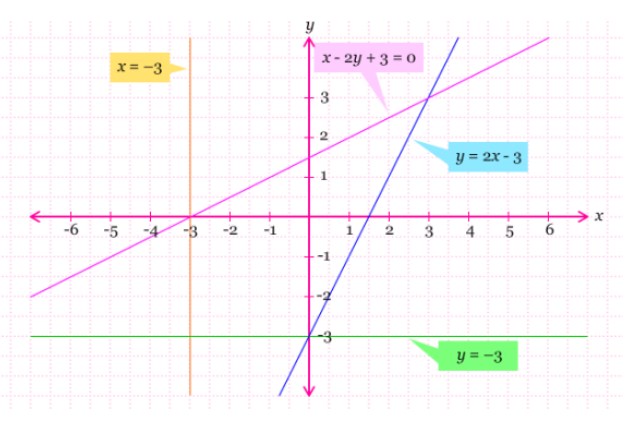
Jadi, jika misalnya ada 1 persamaan garis lurus yang sudah diketahui maka untuk persamaan garis lurus yang sejajar dengan garis itu sendiri akan bisa Anda ketahui. Selanjutnya untuk persamaan garis lurus tersebut mempunyai syarat hubungan gradien. Untuk syarat gradien dan gmbar posisi diantara 2 garis lurus akan kami jelaskan pada pembahasan berikut ini. Mari langsung saja simak pembahasannya di bawah ini.