Rumus Volume Bangun Ruang Lengkap

Rumus Volume Bangun Ruang –  Jika membahas mengenai pelajaran matematika, tentunya Anda sudah asing lagi dengan bangun ruang. Hal ini karena materi mengenai bangun ruang sudah diajarkan sejak kita duduk di bangku Sekolah Dasar atau SD. Bangun ruang sendiri memiliki beberapa jenis dan macam bentuk. Beberapa diantaranya adalah bangun ruang kubus, prisma, balok, bola, tabung, dan lain sebagainya.

Nah, pada kesempatan kali ini kami akan membahas mengenai bangun ruang secara lengkap mulai dari pengertian, macam-macam atau jenisnya, dan juga rumusnya sehingga akan memudahkan Anda dalam mempelajari materi bangun ruang. Untuk lebih jelasnya mari langsung saja simak ulasan selengkapnya berikut ini.

Pengertian Bangun Ruang

Bangun ruang merupakan sebutan untuk beberapa bangun yang memiliki bentuk tiga dimensi atau bangun yang memiliki ruang yang dibatasi oleh sisi-sisinya. Setidaknya ada 7 jenis bangun ruang yang wajib dipelajari dan biasa kita jumpai dalam kehidupan sehari-hari ataupun dalam pelajaran di sekolah.

Pada umumnya, bangun ruang dapat dikategorikan menjadi dua kelompok, yaitu bangun ruang sisi datar dan juga bangun ruang sisi lengkung. Adapun yang termasuk dalam kategori bangun ruang sisi datar adalah kubus, prisma, balok, dan juga limas. Sedangkan untuk bangun ruang sisi lengkung terdiri dari kerucut, tabung, dan juga bola.

Macam-Macam Bangun Ruang

Seperti yang sudah kami jelaskan sebelumnya bahwa bangun ruang mempunyai macam bentuk dengan sifatnya yang berbeda-beda. Beberapa jenis bangun ruang yang akan kita bahas kali ini adalah kubus, balok, prisma, kerucut, tabung dan juga bola. Berikut ini kami akan menjelaskan mengenai rumus dan cara menghitung volume bangun ruang tersebut. Mari langsung saja simak ulasanya dibawah ini.

1. Kubus

Kubus adalah sebuah ruang tiga dimensi yang telah dibatasi oleh enam sisi serupa dalam wujud bujur sangkar. Nama lain dari bangun ruang kubus ini adalah bidang enam beraturan. Bangun ruang kubus sebenarnya merupakan bentuk khusus dari prisma segiempat, karena tingga sama seperti sisi alas.

Sifat Kubus

• Mempunyai 6 sisi dengan bentuk persegi yang mempunyai ukuran sama luas
• Mempunyai 12 rusuk yang mempunyai ukuran sama panjang
• Mempunyai 8 titik sudut
• Mempunyai 4 buah diagonal ruang
• Mempunyai 12 buah bidang diagonal

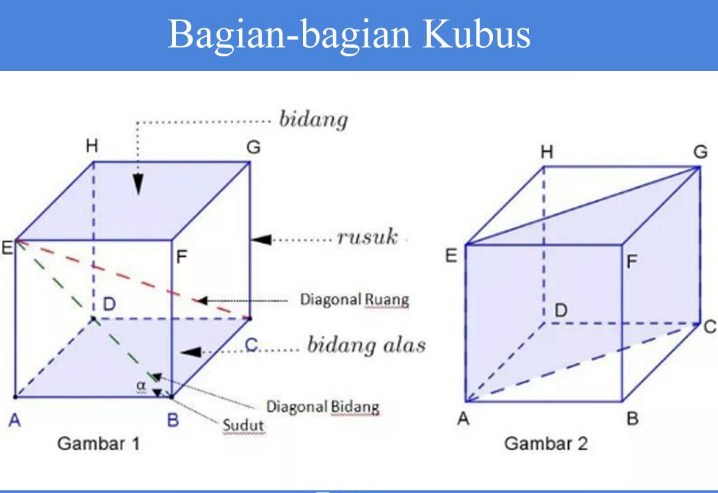
Rumus Pada Kubus

Volume: V= s x s x s = s³
Luas permukaan: 6 s x s = 6 s²
Panjang diagonal bidang: s√2
Panjang diagonal ruang: s√3
Luas bidang diagonal: s²√2

Keterangan:

L= Luas permukaan kubus (cm²)
V= Volume kubus (cm³)
S= Panjang rusuk kubus (cm)

2. Balok

Balok merupakan sebuah bangun ruang yang memiliki tiga pasang sisi segi empat. Masing-masing sisinya yang saling berhadapan memiliki bentuk dan juga ukuran yang sama. Berbeda halnya dengan rumus yang dimana hampir semua kongruen memiliki bentuk persegi, pada bangun ruang balok ini hanya sisi yang saling berhadapan saja yang sama besar. Dan tidak semuanya memiliki bentuk persegi, kebanyakan memiliki bentuk persegi panjang.

Sifat Balok

• Bangun ruang balok memiliki dua pasang sisi dengan bentuk persegi panjang.
• Bagian rusuk yang saling sejajar memiliki ukuran yang sama panjang: AB = CD = EF = GH, dan AE = BF = CG = DH.
• Setiap diagonal bidang pada sisi yang salling berhadapa memiliki ukuran sama panjang, yaitu: ABCD dengan EFGH, ABFE dengan DCGH, dan BCFG dengan ADHE yang mempunyai ukuran sama panjang.
• Setiap diagonal ruang pada balok memiliki ukuran yang sama panjang.
• Setiap bidang diagonalnya memiliki bentuk persegi panjang.

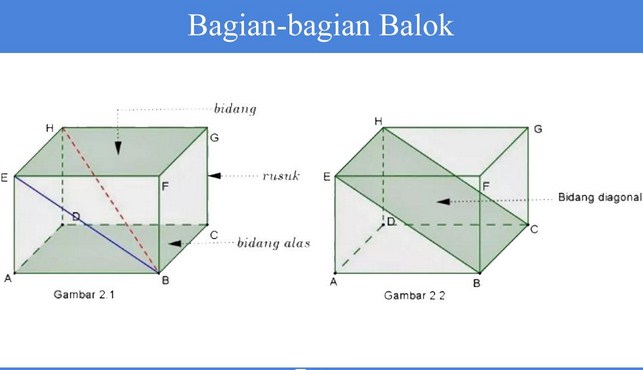
Rumus pada Balok:

Volume: p.l.t
Luas Permukaan: 2 (pl + pt + lt)
Panjang Diagonal Bidang: √(p²+l²) atau juga bisa √(p²+t²) atau √(l²+t²)
Panjang Diagonal Ruang: √(p²+l²+t²)

Keterangan:

p : panjang
l : lebar
t : tinggi

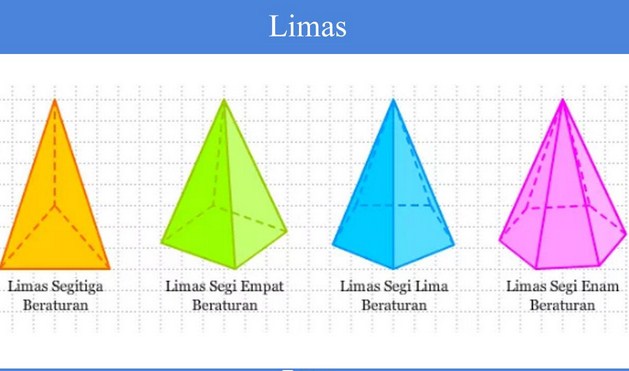
3. Limas

Limas merupakan sebuah bangun ruang tiga dimensi yang telah dibatasi oleh alas dengan bentuk segi-n (bisa berupa segitiga, segiempat, segilima, dan lainnya) dan bidang sisi tegak dengan bentuk segitiga yang saling berpotongan pada satu titik puncak.

Berdasarkan bentuk alasnya, bangun ruang memiliki banyak jenis, yaitu limas segitiga, limas segiempat, limas segi lima dan lainnya. Sebuah bangun ruang limas yang memiliki bentuk lingkaran disebut dengan kerucut. Sedangkan untuk limas dengan alas yang berupa persegi disebut dengan piramida.

Sifat Limas

• Mempunyai 5 sisi yaitu, 1 sisi dengan bentuk segiempat yang berupa alas dan 4 sisi lainnya yang memiliki bentuk segitiga dan merupakan sisi tegak.
• Mempunyai 8 buah rusuk.
• Mempunyai 5 titik sudut, yaitu 4 sudut berada pada bagian alas dan 1 sudutnya berada di bagian atas yang merupakan titik puncak.