Menentukan Nilai Limit X Mendekati 0 – Pembahasan mengenai limit nol biasanya dapat diselesaikan dengan penyelesaian limit pada umumnya. Biasanya, limit dapat dihitung dengan cara substitusi. Cara ini dapat menghasilkan bentuk tentu atau tak tentu. Untuk itu, pada pembahasan limit nol angka x harus dapat mendekati nol agar dapat mendapatkan hasilnya.
Pada dasarnya, limit fungsi adalah perilaku dari suatu fungsi yang mendekati suatu nilai tertentu. Jika suatu fungsi memetakan hasil f(x) untuk setiap nilai x menjadikan fungsi tersebut memiliki limit dimana x mendekati suatu nilai untuk f(x).
Baca juga: Contoh Soal Limit Aljabar: Nilai Limit X
Baca juga: Materi Limit Fungsi Trigonometri
Rumus limit fungsi umumnya memiliki 8 jenis rumus yang dapat diterapkan dalam perhitungannya. Salah satu rumus yang dapat diterapkan adalah limit x mendekati nol. Untuk itu, kali ini kalian akan mempelajari mengenai cara penentuan nilai x mendekati 0. Berikut pembahasannya.
Limit X Mendekati 0
Cara yang paling sering digunakan untuk menentukan nilai limit x mendekati 0 adalah cara substitusi. Cara ini dapat diterapkan pada contoh soal berikut.
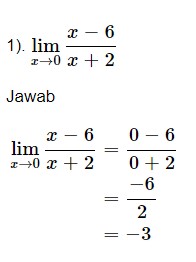
Substitusi di atas dapat dilihat dengan menganti x = 0 dan langsug dimasukkan pada soal tersebut. Kemudian, limit x = 0 dapat diketahui hasilnya yaitu -3.





