Cara Menghitung Simpangan Baku (Standar Deviasi)

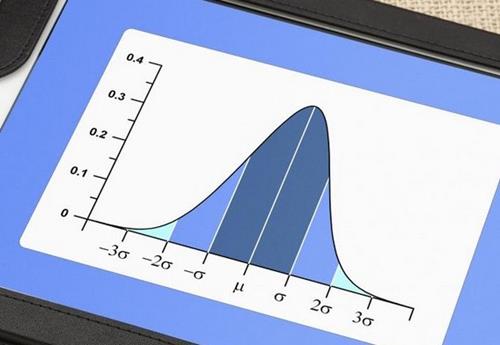
Simpangan Baku – Varian dan standar deviasi (simpangan baku) merupakan ukuran-ukuran variasi yang sering dipakai oleh semua orang. Ini merupakan Standar deviasi (simpangan baku) dari akar kuadrat varian yang sudah sangat lazim digunakan.

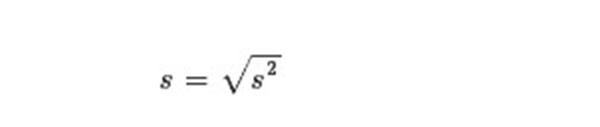
Itulah sebabnya apabila ada salah satu nilai diantara kedua ukuran tersebut sudah anda ketahui maka untuk nilai ukuran yang lain juga bisa diketahui.

Dalam ilmu statistik dan probabilitas, istilah simpangan baku atau standar deviasi cukup sering untuk digunakan. Simpangan baku dapat didefinisikan dengan akar kuadrat varian. Alasannya bilangannya berupa bilangan positif dan mempunyai satuan yang sama dengan sebuah data. Contohnya jika suatu data diukur dengan memakai satuan meter, maka simpangan baku tersebut juga harus diukur dengan memakai satuan meter.

Simpangan baku ini pertama kali diperkenalkan pada 1894 oleh Karl Pearson dalam bukunya On The Dissection Of Asymmetrical Frequency Curves.

Pengertian Simpangan Baku

Simpangan baku adalah suatu teknik statistik yang digunakan untuk menjelaskan homogenitas dalam suatu kelompok.

Selain itu simpangan baku atau standar deviasi juga bisa didefinisikan sebagai nilai statistik yang sering digunakan untuk menentukan bagaimana sebaran data yang ada di dalam sampel, serta seberapa dekat titik dan individu dengan mean atau rata-rata nilai dari sampel tersebut.

Sebelum membahas seputar rumus standar deviasi, ada hal yang perlu kita ingat terlebih dahulu. Nilai simpangan baku dari kumpulan data bisa = 0 atau lebih besar maupun lebih kecil dari nol (0).

Jika nilainya sama dengan nol, artinya semua nilai yang ada dalam himpunan tersebut adalah sama. Sedangkan jika nilainya lebih besar atau lebih kecil, maka dapat disimpulkan bahwa titik data individu tersebut jauh dari nilai rata-rata.

Langkah-langkah Menghitung Simpangan Baku

Ketika ingin mencari nilai simpangan baku, ada beberapa langkah yang perlu dilakukan. Langkah-langkahnya adalah sebagai berikut:

• Menghitung nilai rata-rata setiap titik data yang ada.
• Nilai rata-rata sama dengan jumlah dari setiap nilai yang ada di dalam kumpulan data.
• Setelah itu dibagi dengan jumlah total titik dari data tersebut.
• Langkah selanjutnya adalah menghitung penyimpangan untuk setiap titik data dari rata-ratanya. Caranya adalah dengan mengurangi nilai dari nilai rata-rata.
• Berikutnya, simpangan setiap titik data dikuadratkan dan dicari penyimpangan kuadrat individu rata-ratanya. Nilai yang dihasilkan disebut dengan varian.
• Untuk mencari simpangan baku caranya adalah dengan mengakarkuadratkan nilai varian yang sudah didapat itu.

Fungsi Simpangan Baku

Rumus simpangan baku atau standar deviasi dibuat dengan suatu maksud. Biasanya simpangan baku dimanfaatkan oleh orang-orang yang terjun di dunia statistik untuk mengetahui apakah sampel data yang diambil sudah mewakili seluruh populasi.

Perlu diketahui bahwa mencari data yang tepat untuk suatu populasi sangat sulit untuk dilakukan. Maka dari itu untuk memudahkan kita dalam mencarinya digunakanlah sampel data yang mewakili seluruh populasi. Tujuannya tidak lain untuk memudahkan seseorang dalam melakukan penelitian.

Contohnya kita ingin mengetahui tinggi badan anak-anak yang berusia 8-12 tahun yang ada di suatu wilayah. Maka kita perlu mencari tahu tinggi badan beberapa anak dan menghitung rata-rata dan simpangan bakunya. Dari hasil perhitungan tersebut kita bisa mengetahui nilai yang bisa mewakili seluruh populasi.

Rumus Simpangan Baku

Untuk menentukan dasar penghitungan varian dan simpangan baku merupakan keinginan untuk mengetahui variasi dari kelompok data.

Untuk bisa mengetahui variasi suatu kelompok data yaitu mengurangi nilai data beserta rata-rata kelompok data tersebut, kemudian hasil semuanya baru dijumlahkan.

Hanya saja cara tersebut tidak bisa dipakai karena hasilnya akan selalu menjadi 0.

Supaya nanti hasilnya tidak menjadi 0 yaitu dengan mengkuadratkan setiap pengurangan nilai data serta rata-rata kelompok data tersebut yang kemudian dilakukan penjumlahan. Dengan begitu hasil penjumlahan kuadrat (sum of squares) tersebut akan memiliki nilai positif.

Nilai varian didapat dari pembagian hasil penjumlahan kuadrat (sum of squares) dengan ukuran data (n).

Meskipun demikian ketika diterapkan nilai varian tersebut bias untuk menduga varian populasi. Dengan memakai rumus-rumus diatas maka nilai varian populasi bisa lebih besar dari varian sampel.

Supaya tidak bias saat menduga varian populasi maka n sebagai pembagi penjumlahan kuadrat (sum of squares) harus diganti dengan n-1 (derajat bebas) sehingga nilai varian sampel mendekati varian populasi. Dengan begitu rumus varian sampel akan menjadi seperti dibawah ini:

Nilai varian yang diperoleh merupakan nilai yang berbentuk kuadrat. Seperti misalnya satuan nilai rata-rata adalah gram dengan begitu nilai varian adalah gram kuadrat. Untuk memperoleh nilai satuannya maka varian diakarkuadratkan supaya hasilnya standar deviasi (simpangan baku).

Supaya mempermudah dalam penghitungan maka rumus varian dan simpangan baku tersebut bisa diturunkan :

Rumus varian :

Rumus standar deviasi (simpangan baku) :

Keterangan:

s2 = varian
s   = standar deviasi (simpangan baku)
xi  = nilai x ke-i
   = rata-rata
n   = ukuran sampel

Baca juga : Cara Menghitung Akar Kuadrat

Di atas kita sudah bisa mengetahui bagaimana rumus simpangan baku atau standar deviasi. Sebagai rangkuman berikut beberapa rumus terkait standar deviasi yang bisa disimak. Anda bisa melihat rumus varian, standar deviasi, rumus simpangan baku data tunggal, simpangan baku data berkelompok, dan lain-lain.

Menghitung Standar Deviasi di Excel

Selain dengan cara manual, kita bisa memanfaatkan software pengolah angka seperti Microsoft Excel dan sejenisnya untuk menghitung standar deviasi. Tentu saja caranya akan lebih sederhana dan praktis. Akan tetapi kita perlu mengetahui formula standar deviasi pada Excel.

Untuk menghitung simpangan baku di Excel, kita gunakan rumus STDEV. Sebagai gambaran berikut adalah contoh yang bisa Anda simak.