Cara Menghitung Akar Kuadrat Secara Manual

Menghitung Akar Kuadrat Manual – Pada kesempatan kali ini kita akan membahas mengenai cara mencari akar kuadrat dengan hasil bilangan desimal atau koma.

Saat duduk di bangku sekolah dasar kita akan dihadapkan dengan materi akar kuadrat dalam pelajaran matematika. Dan akar kuadrat ini sangat penting untuk dipelajari karena begitu banyak rumus-rumus matematika yang memiliki akar kuadrat. Tidak hanya dalam pelajaran itu saja, akar kuadrat juga dapat dengan mudah ditemui di dalam ilmu statistik dan lain-lain.

Akar kuadrat atau juga disebut akar pangkat dua bisa dibilang menjadi materi dasar dalam perpangkatan dan akar. Selain akar kuadrat masih ada akar lainnya, seperti akar pangkat tiga. Kita biasanya menggunakan alat bantu seperti kalkulator untuk menghitungnya. Hanya saja ketika ujian tentu kita tidak boleh menggunakan alat tersebut.

Sehingga tidak ada pilihan lain selain menghitungnya secara manual. Dalam menghitung akar kuadrat ada beberapa metode yang bisa kita coba. Mulai dari menerka-nerka bilangan yang tepat dari soal akar kuadrat yang kita hadapi, sampai metode ekstraksi.

Pada kesempatan ini kami bahas lebih lanjut mengenai bagaimana cara mencari akar kuadrat secara manual. Akan tetapi kita awali terlebih dahulu dari mengetahui definisi akar kuadrat itu sendiri. Selamat membaca pembahasan berikut ini.

Baca juga: Cara Menghitung Akar Pangkat 3

Apa itu Akar Kuadrat

Dalam matematika diketahui bahwa kuadrat merupakan hasil perkalian suatu bilangan dengan bilangan itu sendiri. Namun akar kuadrat atau akar pangkat 2 adalah kebalikan dari kuadrat atau invers pangkat 2 dari suatu bilangan. Akar kuadrat dalam bahasa Inggris disebut “square root” dan biasanya ditandai dengan tanda “√”.

Jika dinyatakan nilai akar kuadrat suatu bilangan x adalah y maka berlaku x = y², dengan catatan x dan y merupakan bilangan real. Maka juga dapat kita tulis dengan √x = y atau dibaca “akar kuadrat dari x sama dengan y”.

Metode Perhitungan Akar Kuadrat Bilangan Bulat

Ada beberapa cara yang bisa diterapkan dalam mencari akar kuadrat suatu bilangan bulat. Berikut kami jelaskan secara singkat. 

Dengan cara perkalian

Pertama-tama carilah angka atau bilangan bulat yang bisa dikalikan dengan dirinya sendiri terlebih dahulu. Hal ini dikarenakan, akar kuadrat sebuah bilangan bulat merupakan suatu bilangan yang jika dikalikan dengan bilangan yang sama maka hasilnya adalah angka yang semula.

Contoh: diketahui akar kuadrat dari 1 yaitu 1 karena 1 dikalikan 1 sama dengan 1. Begitu juga dengan akar kuadrat dari 4 adalah 2 karena 2 dikalikan 2 sama dengan 4. Dan seterusnya dengan bilangan-bilangan bulat lainnya.

Dengan cara pembagian bersusun

Cara untuk menghitung akar kuadrat bisa juga dengan menggunakan pembagian bersusun. Pembagian akan lebih memudahkan dalam menghitung karena prosesnya jelas dan tidak perlu menerka-nerka. Hanya perlu menyusun dengan urutan yang benar. Jadi untuk mencari akar kuadrat dari bilangan bulat kalian tinggal membagi bilangan itu sampai mendapatkan hasil atau jawabannya.

Perlu diketahui, untuk bilangan bulat akar kuadratnya tidak memiliki pecahan atau desimal.

Contoh: jika 16 : 4 = 4, maka 4 : 2 = 2 dan seterusnya. Maka akar kuadrat dari 16 adalah 4 dan akar kuadrat dari 4 adalah 2.

Dengan menggunakan simbol untuk kuadrat

Cara lain untuk memudahkan dalam mencari akar kuadrat adalah menggunakan symbol. Simbol akar kuadrat sudah digunakan sejak dahulu oleh para matematikawan.

Seperti yang sudah diketahui sebelumnya, bentuk simbolnya yaitu seperti tanda centang “√”. Penggunaan simbol ini biasanya dengan meletakkan nilai N di bawah tanda centang. Dimana N merupakan bilangan yang akan dicari nilai akar kuadratnya.

Semisal untuk mencari akar kuadrat dari 4, maka tuliskan rumusnya yaitu dengan meletakkan nilai N (4) di dalam tanda centang tersebut.  Kemudian tuliskan secara langsung simbol yang sama dan ditulis dengan angka 2 yang artinya akar kuadrat dari 4 adalah 2.

Contohnya: √4 = 2, maka 4 : 2 = 2

Cara Menghitung Akar Kuadrat

Sebagai contoh soal misalnya apabila akar kuadrat dari 124 ?

• penyelesaiannya adalah kita cari 2 jawaban terdekat dari akar kuadrat 124, maka akan kita temukan hasil sementara 11 dan 12

• 11^2 = 121 —-> kurang dari 124 / lebih kecil

• 12^2 = 144 —-> terlalu besar

• kesimpulan sementara jawaban nya adalah 11 koma

• kemudian kita cari selisih antara 124 dan 121 ——> 124-121 = 3

• kemudian kita cari selisih kedua nilai terdekat 144 dan 121 ——> 144-121 = 23

• jadi kita peroleh pecahannya adalah 3/23

• sehingga di dapatkan jawaban akar dari 124 adalah 11 + 3/23 = 11,13

Kemudian jika menggunakan cara kedua dalam cara menghitung akar kuadrat dengan hasil desimal bisa memakai cara pemfaktoran, anda bisa melihat detailnya dibawah ini :

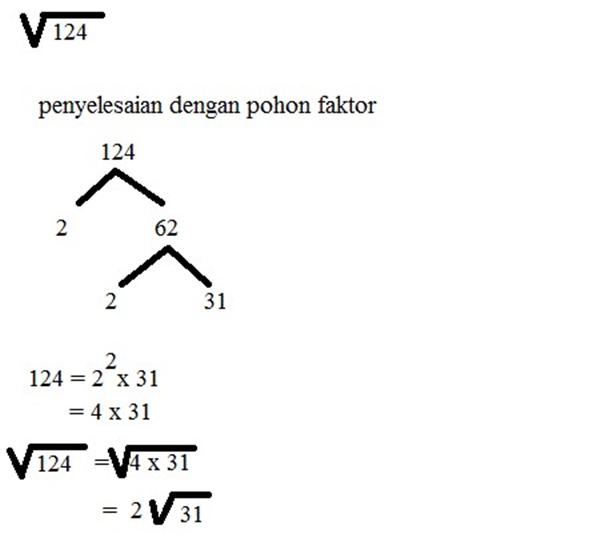
Pada cara kedua tersebut bisa memakai pohon faktor yaitu 124 di bagi 2 hasilnya 62, lalu di bagi 2 yang nantinya akan diperoleh angka 31 yang sudah tidak bisa dibagi lagi sehingga diperoleh hasil akhir 124 = 2^2 x 31
Dengan begitu V 124 = V 2^2 x V 31 = 2V31

Apabila masih bingung, bisa memakai cara manual seperti yang akan saya berikan dibawah ini :