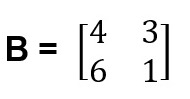Pengertian Transpose Matriks Dan Contoh Soal

Pengertian Transpose Matriks Dan Contoh Soal – Selain ada operasi penjumlahan, pengurangan, dan perkalian, pada matriks matematika kita juga akan mempelajari yang disebut transpose matriks. Pada beberapa kesempatan sebelumnya kalian sudah mempelajari bahwa matriks adalah sekumpulan bilangan yang diletakkan di dalam tanda kurung dan disusun berjajar sehingga memiliki baris dan kolom.

Pada matriks tanda kurung yang digunakan bisa berupa “()” atau tanda kurung siku “[]”. Sedangkan nama matriks umumnya berupa huruf kapital, seperti A, B, C, D, E, dan seterusnya. Baris merupakan susunan yang dibuat horizontal atau mendatar. Sedangkan kolom merupakan susunan yang dibuat vertikal. Penamaan baris dan kolom pada matriks dibuat berurutan.

Mulai dari yang paling atas dinamakan baris ke-1, baris ke-2 di bawahnya, dan seterusnya. Begitu juga kolom yang dimulai dari yang paling kiri dan diberi nama kolom ke-1, lanjut kolom ke-2, dan seterusnya.

Baca juga: Penjumlahan Dan Pengurangan Matriks

Apa itu Transpose Matriks

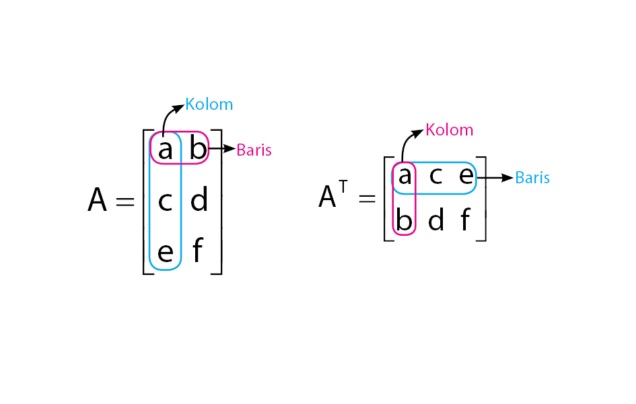
Setelah membahas sedikit tentang matriks, kini kita bahas materi tentang transpose matriks. Transpose matriks dapat diartikan sebagai suatu matriks yang dikerjakan dengan cara pertukaran antar dimensi kolom dan baris. Pengertian lain dari transpose matriks adalah suatu matriks yang diperoleh dengan memindahkan elemen-elemen pada suatu kolom menjadi elemen-elemen pada suatu baris, dan demikian pula sebaliknya.

Dari kedua pengertian tersebut dapat kita simpulkan bahwa transpose matriks dapat kita ketahui dengan mengubah kolom menjadi baris dan sebaliknya. Matriks transpose ini dilambangkan dengan “T” kecil yang diletakkan di atas nama matriks.

Seperti yang sudah dijelaskan di atas, transpose matriks dilakukan dengan mengubah letak kolom dan baris. Contohnya adalah sebagai berikut.