Contoh Soal Penjumlahan Pengurangan Matriks – Materi seputar matriks biasanya diajarkan saat kita duduk di bangku SMA. Jika kalian masih asing, matriks merupakan susunan suatu bilangan-bilangan yang berbentuk persegi panjang dan diatur dalam baris atau kolom yang dibatasi tanda kurung.
Pada matriks baris merupakan bilangan-bilangan yang disusun mendatar atau horizontal, sementara kolom merupakan susunan bilangan yang diatur tegak atau vertikal.
Sekilas mungkin kalian menganggap materi ini tidak ada gunanya. Akan tetapi sebenarnya matriks matematika ini bisa digunakan dalam sistem komputer.
Sebab matriks bisa dipakai sebagai pemrograman yang memerlukan array. Matriks juga bisa dimanfaatkan untuk membuat suatu enkripsi data.
Dalam matriks kita juga mengenal operasi hitung jumlah, kurang, dan kali. Pada matriks tidak ada operasi pembagian, dan diganti dengan invers matriks.
Melihat susunannya yang terlihat unik, bagaimana cara menjumlahkan dan mengurangkan dua matriks? Yuk kita pelajari penjumlahan dan pengurangan matriks di bawah ini.

Baca juga: Pengertian Transpose Matriks Dan Contoh Soal
Penjumlahan Matriks
Penjumlahan matriks berbeda dengan penjumlahan pada bilangan bulat. Sebab ada syarat tertentu yang harus terpenuhi sebelum kedua matriks bisa dijumlahkan. Dua atau lebih matriks baru bisa dijumlahkan apabila mempunyai nilai ordo yang sama. Dengan kata lain seluruh matriks yang dijumlahkan harus mempunyai jumlah kolom dan baris yang sama persis.
Lebih jelasnya matriks dengan jumlah baris 2 dan kolom 3 hanya dapat dijumlahkan dengan matriks yang memiliki 2 baris dan 3 kolom. Dan begitu seterusnya.
Di samping itu penjumlahan matriks juga mempunyai beberapa sifat, seperti komutatif, asosiatif, serta mempunyai matriks identitas matriks nol dan mempunyai lawan matriks.
Untuk dicatat, lawan matriks A adalah matriks -A. Artinya elemen-elemen pada matriks -A adalah lawan dari elemen-elemen matriks A. Berikut adalah beberapa sifat operasi penjumlahan Matriks.
Sifat Penjumlahan Matriks
-
Komutatif: A + B = B + A
-
Asosiatif: (A + B) + C = A + (B + C) = A + B + C
-
Matriks nol merupakan matriks identitas penjumlahan, sehingga berlaku: A + 0 = 0 + A = A
-
Matriks identitas pada penjumlahan matriks -A: A + (-A) = (-A) + A = 0
Setelah mengetahui sekilas tentang apa itu penjumlahan pada matriks dan sifat-sifatnya, sekarang kita lihat bagaimana cara menjumlahkan dua atau lebih matriks. Silakan simak ilustrasi berikut.
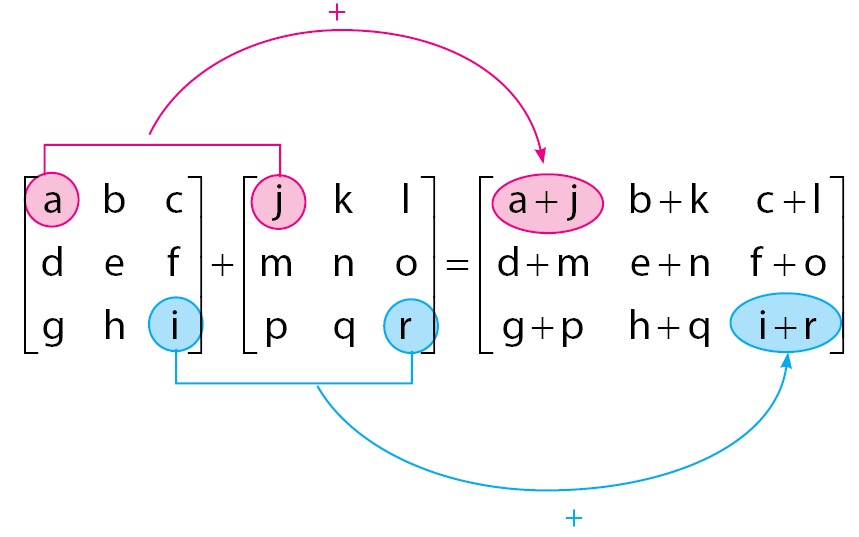
Di atas merupakan gambaran mengenai cara menjumlahkan dua matriks. Caranya pun mudah, kita tinggal menjumlahkan masing-masing baris dan kolom dengan matriks selanjutnya saja.
Misalnya baris satu kolom satu pada matriks pertama dijumlahkan dengan baris satu kolom satu pada matriks kedua, dan seterusnya.
Baca juga: Perkalian Matriks Dan Contoh Soal
Pengurangan Matriks
Berikutnya kita bahas bagaimana cara melakukan operasi pengurangan matriks. Syarat pengurangan matriks matematika ini sama dengan penjumlahan. Yakni dua atau lebih matriks yang akan dikurangkan harus mempunyai nilai ordo yang sama. Untuk cara mengurangkan matriks bisa dilihat pada rumus berikut.
A – B = A + (-B)
Mengerjakan operasi pengurangan pada matriks mirip dengan penjumlahan. Kita tinggal mengurangi masing-masing elemen dari matriks pertama dengan elemen pada matriks kedua. Gambarannya bisa kalian lihat di bawah ini.




