Tabel Distribusi Normal – Pembelajaran statistik menjadi salah satu hal dasar yang perlu dipahami ketika mengolah data. Pengolahan data pada sebuah penelitian perlu dilakukan dengan konsep yang baik sehingga penerapannya tidak terasa rumit. Salah satu penghitungan data yang sering dilakukan saat mengolah data adalah pengolahan tabel distribusi normal.
Pengolahan tabel distribusi normal diterapkan pada data kuantitatif yang berupa angka dan perlu dilakukan perhitungan lebih lanjut. Data kuantitatif merupakan jenis data yang dapat diukur atau dihitung sehingga dapat diubah menjadi sebuah informasi. Hal ini dapat menggunakan distrbusi normal yang ditransformasikan membentuk tabel z.

Baca Juga: Cara Menghitung T Tabel dan Contohnya
Baca Juga: Tabel Chi Square Tutorial Lengkap
Baca Juga: Cara Membuat R Tabel Product Moment
Pada pembahasan kali ini kalian akan mempelajari mengenai tabel distribusi normal. Berikut pembahasannya.
Definisi tabel distribusi normal
Pada pengolahan data menggunakan distribusi normal, terdapat hal yang membahas mengenai tranformasi yang dilakukan sampai distribusi normal tersebut mempunyai rata-rata 0 dan varian 1. Tabel distribusi normal memiliki isi peluang dari nilai Z atau P (Z ≤ z). Hal ini dapat dipahami bahwa nilai peluang selalu ada di antara 0 dan 1, sampai nilai di dalam tabel ada diantara 0 dan 1.
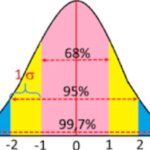
Pembahasan distrbusi normal menjadi salah satu jenis distribusi dengan variabel acak yang kontinu. Pada distribusi normal terdapat kurva/grafik yang digambarkan menyerupai bentuk lonceng. Distribusi normal dapat disebut juga sebagai distribusi Gauss. Persamaan yang terdapat dalam distribusi normal salah satunya yaitu terkait fungsi densitas.
Rumus distribusi normal
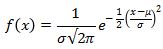
Keterangan:
π : konstanta dengan nilai 3,14159. . .
e : bilangan eksponensial dengan nilai 2,7183 . . .
µ : rata-rata (mean) dari data
σ : simpangan baku data berdistribusi normal
Kemudian, nilai z dapat dihitung dengan rumus berikut.
Baca Juga: Cara Membuat R Tabel Uji Validitas
Baca Juga: R Tabel dalam Statistika dan Contohnya
Baca Juga: Cara Membuat Ogive Dari Tabel Distribusi Frekuensi
z = (x – µ)/σ
Keterangan:
µ : rata-rata (mean) dari data
σ : simpangan baku data berdistribusi normal