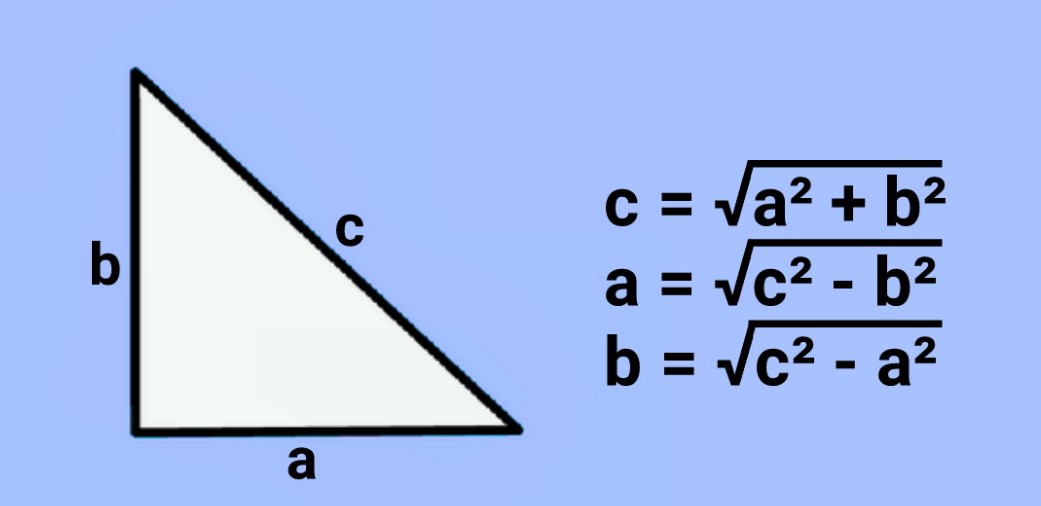Konsep Sudut Segitiga Siku-Siku dalam Trigonometri

Baca juga: Sudut Sehadap, Berseberangan, Sepihak, dan Contohnya

Rumus Phytagoras Segitiga Siku-Siku

Rumus Phytagoras dapat diterapkan apabila salah satu sisi segitiga siku siku tersebut belum diketahui. Penggunaan rumus ini digunakan untuk mendapatkan panjang sisi yang belum diketahui tersebut dan harus diperhatikan bagian mana yang perlu dimasukkan pada rumusnya. Berikut merupakan rumus Phytagoras.

c² = a² + b²  atau  c = √a² + b²

a² = c²– b²  atau  a = √c² – b²

b² = c² – a²  atau  b = √c² – a²

Demikian pembahasan singkat mengenai konsep pada segitiga siku-siku. Semoga materi kali ini dapat bermanfaat dan jangan lupa untuk senantiasa belajar, ya.