Sudut Sudut Istimewa – Salah satu materi dalam pelajaran Matematika yang wajib di pahami adalah sudut istimewa. Sudut ini biasa disebut dengan sudut istimewa karena dapat diukur dengan sangat mudah, yaitu hanya menggunakan perbandingan trigonometri.
Ada lima sudut istimewa dalam trigonometri yang perlu Anda ketahui, yaitu 0°, 30°, 45°, 60°, dan 90°. Nah, berikut ini kami akan menjelaskan secara detail mengenai sudut-sudut istimewa tersebut. Namun sebelum itu kami akan membahas terlebih dahulu mengenai pengertian trigonometri sebagai dasar materi.
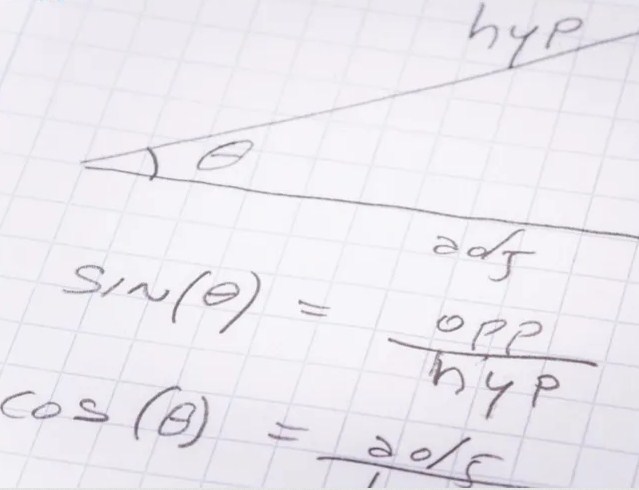
Pengertian Trigonometri
Trigonometri adalah salah satu cabang ilmu Matematika yang secara khusus hanya mempelajari tentang hubungan antar sisi dan sudut sebuah segitiga. Hubungan ini mencakup relasi dan juga fungsi dasar yang muncul. Saat melakukan perhitungan, trigonomerti adalah nilai perbandingan yang didapatkan pada segitiga siku-siku ataupun koordinat kartesius.
Adapun fungsi dasar trigonometri adalah sin (sinus), cos (cosines), tan (tangen), cosec (cosecant), sec (secant) dan juga cotan (cotangen). Fungsi dasar yang satu ini adalah cara yang digunakan untuk dapat menemukan besarnya sudut ataupun sisi dari suatu segitiga.
Sebelum masuk ke pembahasan sudut istimewa yang lebih spesifik, perlu Anda ketahui bahwa sebuah bangun datar segitiga memiliki tiga buah sisi, yaitu sisi samping, sisi depan dan sisi miring. Sementara itu, jika ketiga sudutnya dijumlahkan maka harus berjumlah 180°.
Ketiga sisi yang dimiliki oleh bangun datar tersebut berguna untuk menghitung fungsi trigonometri. Untuk melakukan perhitungan sin, maka sisi depan harus dibagi dengan sisi miring. Untuk melakukan perhitungan cos, sisi samping harus dibagi dengan sisi miring. Sedangkan untuk menentukan nilai tan, maka sisi depan harus dibagi dengan sisi miring.
Sementara itu, untuk menghitung cosec yaitu 1/sinα. Untuk melakukan perhitungan sec adalah 1/cosα. Dan yang terakhir adalah untuk menghitung cot, yakni dengan rumus 1/tanα.
Baca Juga: Rumus Dan Contoh Soal Identitas Trigonometri
Pengertian Sudut Istimewa

Lalu apa yang dimaksud dengan sudut istimewa? Jika Anda masih mengalami kebingungan maka kami akan menjelaskan pengertian sudut istimewa lebih dulu. Seperti yang sudah kami jelaskan diatas bahwa sudut istimewa merupakan sebuah sudut dengan nilai perbandingan trigonometri yang bisa ditentukan berapa nilainya tanpa perlu menggunakan kalkulator.
Sudut-sudut istimewa dalam trigonometri adalah 0°, 30°, 45°, 60°, dan 90° dan seterusnya. Penting untuk diketahui bahwa sudut istimewa ini ternyata memiliki keistimewaan. Jika ditanya berapakah nilai dari sin 23°, apakah yang Anda lakukan? Mungkin Anda akan menghitung nilainya dengan menggunakan rumus atau grafik, bertanya kepada teman dan guru, atau menghitung dengan menggunakan kalkulator.
Pada umumnya memang untuk mencari nilai dari sinus, cosinus, ataupun tangen pada sudut yang tertentu kita akan membutuhkan alat bantu berupa kalkulator untuk dapat menemukan jawaban secara tepat. Namun untuk beberapa sudut yang tertentu kita tidak membutuhkan alat bantu hitung. Nah, sudut inilah yang kemudian disebut dengan sudut istimewa.
Pengertian Sin Cos Tan
Selanjutnya kami akan membahas pengertian sin cos tan terlebih dahulu supaya Anda nantinya tidak mengalami kebingungan. Berikut ini adalah pengertian dari sin cos tan:





