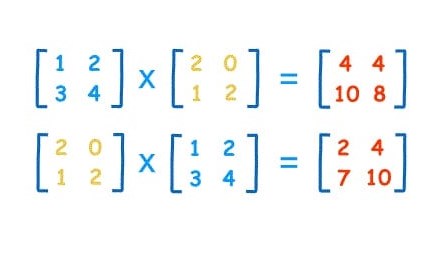Contoh Soal Dan Jawaban Matriks Kelas 11 SMA-SMK

Contoh Soal Matriks Kelas 11 – Pernahkah kalian mengamati pola baris atau kolom pada sebuah susunan keramik? Apakah kalian tahu bahwa susunan tersebut dapat diaplikasikan pada sebuah pola matematika, yaitu matriks?

Materi matriks sebelumnya sudah dipaparkan di kelas 10. Agar dapat mengingat kembali mengenai materi matriks, berikut akan diulas secara singkat mengenai materi matriks dan beberapa contoh soal matriks di kelas 11.

Baca juga: Materi Dan Contoh Soal Matriks Kelas 10

Matriks dalam pola matematika berarti susunan bilangan yang diatur berdasarkan aturan baris dan kolomnya. Biasanya, matriks dibentuk persegi atau persegi panjang bergantung pada ordo penyusunnya. Penyusunannya dapat diletakkan di dalam kurung biasa () atau kurung siku []. Penggunaan nama pada matriks dapat menggunakan huruf kapital, seperti A, B, C, dan seterusnya. Agar lebih mudahnya memahami matriks, berikut contoh kecil masalah dalam kehidupan sehari-hari untuk menerapkan matriks.

Sebuah karyawan bertugas untuk menata beberapa stok barang yang akan dipajang di etalase toko. Susunan barang yang terlalu banyak menyulitkan karyawan dalam menyusunnya dan memerlukan waktu cukup lama. Berikut susunannya.

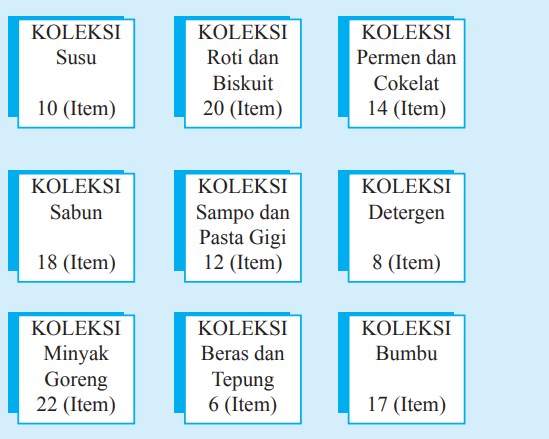
Susunan barang pada rak di atas dapat disusun dengan pola matriks yang terdiri atas tiga baris dan tiga kolom seperti berikut.

Matriks juga memiliki beberapa detail penyusunnya yang berbeda sehingga dibagi menjadi beberapa jenis. Secara detail, jenis matriks terdiri atas matriks baris, kolom, persegi panjang, persegi, segitiga, diagonal, identitas, dan nol.

Dalam dua tampilan matriks, terdapat kemungkinan terjadi kesamaan. Hal ini dapat disebabkan dengan adanya kesamaan ordo atau elemen dari matriks. Matriks A dan B dapat dikatakan sama (A = B) dengan adanya ordo yang sama dan entry yang seletak memiliki nilai sama seperti berikut.

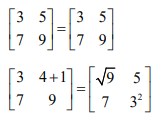
Baca juga: Materi dan Contoh Soal Matriks Pangkat

Operasi pada matriks dapat berupa operasi aljabar. Pada operasi penjumlahan pada matriks, dua atau tiga matriks yang dapat dijumlahkan hanya jika memiliki ordo sama. Ordo matriks hasil penjumlahan dua matriks dapat disimpulkan sama dengan ordo matriks yang dijumlahkan. Hal ini pun berlaku pada operasi pengurangan. Pengurangan pada matriks didefinisikan sebagai jumlah antara matriks A dengan matriks –B. Hal ini pun dapat ditulis A – B = A + (-B).

Operasi aljabar perkalian pada matriks biasanya menyebutkan bilangan real k dengan sebutan skalar. Hal ini pun menjadikan perkalian matriks disebut sebagai perkalian skalar dengan matriks. Umumnya, perkalian skalar dapat berwujud matriks ordo m x n dengan entry a_ij dan k sebagai bilangan real. Hasil perkalian berupa matriks C merupakan bilangan real k terhadap matriks A dan dinotasikan C = k.A.

Lalu, operasi aljabar perkalian terdapat perkalian dua matriks yang dimisalkan A_{m x n} dan matriks B_{n x p} matriks A dapat dikalikan B. Hasil perkalian matriks A dengan ordo m x n dengan matriks B ordo n x p akan menjadikan matriks berordo m x p.

Transpose matriks dapat terjadi apabila ada perubahan pada posisi entry matriks seperti baris ke-1 menjadi kolom ke-1. Sebuah transpose dari matriks A dengan ordo m x n akan memperoleh matriks A yang bertukar entry baris menjadi kolom sehingga ordo terbalik menjadi n x m.

Determinan pada matriks biasanya berhubungan dengan sistem persamaan linear. Hal ini akan lebih memudahkan penyelesaikan dalam menentukan himpunannya. Pada konsep matriks, nilai (a₁.b₂ – a₂.b₁) sebagai sebuah determinan matriks. Hal ini pun berhubungan dengan notasi dan sifat determinan.