Sifat Bilangan Berpangkat Dan Contohnya

Sifat Bilangan Pangkat Dan Contohnya – Dalam matematika kita bisa mengetahui banyak jenis bilangan. Ada yang familiar, dan juga ada yang asing. Salah satu jenis bilangan yang bisa kita kenal dengan mudah adalah bilangan berpangkat. Mungkin saat pertama kali mempelajarinya kalian merasa sudah kesulitan. Padahal sebenarnya bilangan ini justru berfungsi untuk menyederhanakan penulisan.

Perlu kalian ketahui bahwa bilangan berpangkat ditemukan oleh John Napier seorang bangsawan dari Merchiston, Skotlandia di tahun 1500-an. Di samping itu perkalian berulang yang ditulis dalam bentuk bilangan berpangkat juga dikemukakan oleh Rene Descartes, seorang ahli matematika asal Perancis.

Bilangan berpangkat adalah perkalian berulang suatu bilangan, dimana bilangan tersebut bisa berupa berpangkat bulat positif, bulat negatif, atau nol. Pada bilangan ini terdapat beberapa sifat yang perlu kita ketahui. Nah pada kesempatan ini kita bahas lebih jauh seputar hal tersebut.

Baca juga: Penjumlahan Dan Pengurangan Bilangan Berpangkat

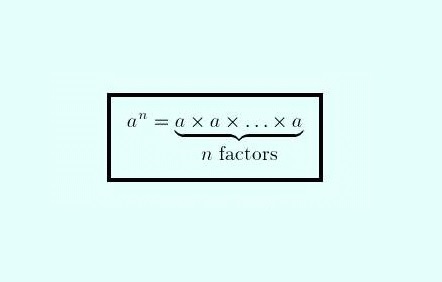
Sifat Bilangan Berpangkat

Di atas sudah disinggung bahwa bilangan berpangkat terbagi menjadi beberapa macam. Maka dari itu sifat bilangan berpangkat juga tergantung dari jenis bilangan berpangkat itu sendiri. Apakah bilangan berpangkat bulat positif, nol, ataupun bulat negatif.

Sifat Pangkat Bulat Positif

Bilangan berpangkat positif merupakan bilangan dengan pangkat atau juga disebut eksponen positif. Bilangan ini mempunyai beberapa sifat Seperti terdiri dari a, b, bilangan real m, dan n yang merupakan bilangan bulat positif. Berikut adalah beberapa sifat dari bilangan pangkat bulat positif:

• am x an = am+n
• am : an = am-n, untuk m > n 
• (am)n = amn
• (ab)m = ambm
• (a/b)m = am/bm, untuk b ≠ 0

Agar tidak bingung dengan sifat-sifat di atas, akan kami berikan penjelasan. Misalnya pada sifat pertama ada am × an = am+n. Sifat ini berlaku apabila a adalah bilangan real, sedangkan m dan n adalah bilangan bulat positif. Jika m dan n bukan bilangan bulat positif, maka sifat tersebut tidak berlaku lagi.

Contoh:

22 x 23 = (2 x 2) x (2 x 2 x 2)

= 32

= 25

22 x 23 = 22+3

Sifat kedua ada am : an = am-n, yang artinya pembagian dua bilangan berpangkat positif dengan ketentuan a adalah bilangan real yang sama, serta m dan n merupakan bilangan bulat positif, maka kita bisa mengurangi pangkat keduanya atau m dikurangi n.

Contoh:

25 / 23 = 2 x 2 x 2 x 2 x 2 / 2 x 2 x 2