Rumus Tripel Pythagoras dan Contoh Soalnya – Salah satu bangun datar yang memiliki keistimewaan adalah segitiga. Keistimewaan segitiga berkaitan dengan sudutnya, terutama pada segitiga siku-siku yang memiliki teorema Pythagoras. Hal ini berhubungan dengan keterkaitan sisi-sisi segitiga.
Penerapan Pythagoras biasanya dapat digunakan dalam kehidupan sehari-hari. Misalnya, dalam pembentukan pondasi bangunan hingga kerangka atap. Hal ini juga dapat digunakan untuk menentukan jarak terdekat dari dua posisi benda yang berbentuk segitiga menggunakan teorema Pythagoras.

Baca juga: Cara Mencari Panjang Sisi Segitiga Lengkap
Baca juga: Rumus Luas Permukaan Balok Dan Volume Balok
Secara sederhana, teorema Pythagoras menyatakan bahwa kuadrat sisi miring segitiga siku-siku (hipotenusa) sama dengan jumlah kuadrat sisi-sisi yang saling berpenyiku. Sisi terpanjang segitiga siku-siku dikuadratkan maka akan sama dengan jumlah dari kuadrat sisi yang lainnya.
Kali ini kalian akan mempelajari mengenai teorema Pythagoras yang diuraikan berdasarkan rumusnya. Berikut pembahasannya.
Rumus Pythagoras
Rumus Pythagoras dapat kita lihat pada segitiga siku-siku yang memiliki ukuran sisi masing-masing dari sisi a, b, dan c.
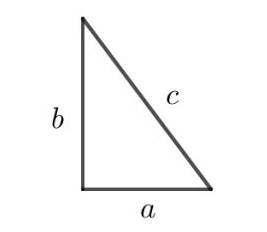
Inti dari rumus Pythagoras adalah a2 + b2 = c2. Berdasarkan gambar di atas, dapat diketahui keterangannya sebagai berikut.
- Jika a2 + b2 < c2 maka jenis segitiganya adalah segitiga lancip.
- Jika a2 + b2 > c2 maka jenis segitiganya adalah segitiga tumpul.
- Jika a2 + b2 = c2 maka jenis segitiganya adalah segitiga siku-siku.
Baca juga: Rumus Persegi Panjang Luas Dan Kelilingnya Lengkap




