Materi Rumus Matriks Matematika SMA

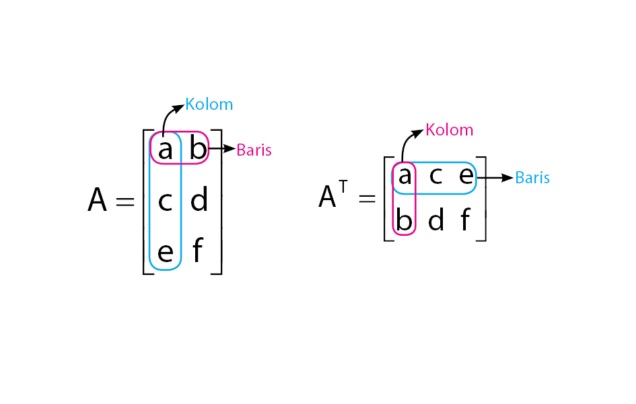
Pada suatu model matriks, kita juga perlu mengetahui mengenai ordo matriks. Ordo matriks merupakan bilangan asli yang menyatakan banyaknya baris dan kolom dari matriks tersebut. Seperti matriks A memiliki m baris dan n kolom dapat dinyatakan sebagai matriks A berordo m x n. Untuk m = n dapat dinyatakan sebagai matriks A berordo n.

Sebuah matriks diberi lambang dengan huruf kapital, seperti A, B, dan seterusnya, sedangkan elemen matriks diberi lambang dengan huruf kecil berindeks, yaitu aij dengan 1 ≤ i ≤ m, 1 ≤ j ≤ n, m dan n menyatakan banyaknya baris serta banyaknya kolom.

Jadi, inti dari matriks merupakan jajaran bilangan-bilangan berbentuk persegi panjang atau persegi yang tersusun dalam baris dan kolom yang terletak di dalam kurung biasa ( ) atau kurung siku [   ].

Baca juga: Penjumlahan Pengurangan Matriks Dan Contoh Soal

Baca juga: Perkalian Matriks Dan Contoh Soal Lengkap

Macam-Macam Matriks

Dari pengertian matriks, dapat kita pahami bahwa matriks pastinya memiliki baris dan kolom sebagai penyusunnya. Namun, perlu kita ketahui bahwa matriks memiliki berbagai macam jenisnya dan dibagi menjadi beberapa jenis. Berikut akan diuraikan mengenai macam-macam matriks.

1. Matriks nol
   Matriks nol merupakan matriks yang semua elemennya memiliki nilai nol.
2. Matriks baris
   Matriks baris merupakan matriks yang hanya terdiri atas satu baris saja.
3. Matriks kolom
   Matriks kolom merupakan matriks yang terdiri atas satu kolom.
4. Matriks persegi
   Matriks persegi merupakan matriks yang banyak baris dan banyak kolomnya sama.
5. Matriks segitiga atas
   Matriks segitiga atas merupakan matriks persegi yang elemen di bawah diagonal utamanya bernilai nol.
6. Matriks segitiga bawah
   Matriks segitiga bawah merupakan matriks persegi yang elemen di atas diagonal utamanya bernilai nol.
7. Matriks diagonal
   Matriks diagonal merupakan matriks persegi yang elemen-elemennya bernilai nol, kecuali pada diagonal utamanya tidak selalu nol.
8. Matriks identitas
   Matriks identitas merupakan matriks skalar yang elemen-elemen pada diagonal utamanya bernilai 1.

Baca juga: Contoh Soal Dan Rumus Matriks Invers

Rumus Dasar Matriks

Rumus dasar dalam menyelesaikan perhitungan matriks dapat menggunakan materi dasar operasi aljabar. Operasi aljabar ini menjadi dasar untuk memahami perhitungan matrik, mulai dari proses perhitungan penjumlahan, pengurangan, dan perkalian. Berikut pembahasannya.

1. Penjumlahan pada matriks

Aturan dasar dalam melakukan penjumlahan pada dua buah matriks adalah ordo yang sama. Jika ordo matriks tidak sama menjadikan operasi penjumlahan tidak dapat dihitung selesai. Misalnya saja ordo matriks A = 2 x 3 dan ordo matriks B = 2 x 3 maka keduanya dapat dijumlahkan.

Penjumlahan pada operasi matriks memiliki hal-hal dasar dengan beberapa sifat berikut.

• A + B = B + A (sifat komutatif)
• A + (B + C) = (A + B) + C (sifat asosiatif)
• Terdapat matriks identitas penjumlahan, yaitu matrik nol sehingga berlaku A + 0 = 0 + A = A untuk setiap matriks A.
• Terdapat invers penjumlahan sehingga berlaku A + (- A) = – A + A = 0. Matriks– A atau matriks lawan dari matriks A adalah matriks yang elemen-elemennya merupakan negatif dari elemen dari matriks A yang seletak.

2. Pengurangan pada matriks

Aturan dasar pada operasi pengurangan matriks memiliki prinsip sama dengan operasi penjumlahan sebuah matriks. Dengan begitu, pada operasi pengurangan matriks juga memiliki sifat sama dengan mengganti tandanya saja sebagai berikut.

• A – B = A + (- B)
• A – B = C
• A + B = C maka berarti B = C – A dan A = C – B.

3. Perkalian pada matriks

Operasi aljabar perkalian dapat diterapkan pada matriks apabila terjadi di antara matriks dengan suatu skalar atau dapat dilakukan dengan perkalian antarmatriks atau matriks dengan matriks.

• Perkalian antara matriks dengan skalar
  Jika A suatu ordo m n dan k suatu bilangan real (disebut juga suku skalar), maka A adalah matriks ordo m n yang unsur-unsurnya diperoleh dengan memperkalikan setiap unsur matriks A dengan k. Perkalian seperti ini disebut perkalian skalar. Dalam melakukan perkalian matriks juga terdiri atas beberapa sifat-sifat berikut.
  1) (a + b)A = aA + bA
  2) a (A + B) = aA + aB
  3) a(bA) = (ab)A
  4) 1 × A = A
  5) 0 × A = 0
  6) (- 1) A = – A
• Perkalian antarmatriks
  Perkalian antarmatriks misalnya dapat dilakukan dengan matriks A yang berordo m p dangan suatu matriks B yang berordo p n adalah matriks C yang berordo m n. Dengan begitu menjadi A m p.B p n = C m n. Dalam perkalian antarmatriks ini yang perlu diperhatikan adalah banyaknya kolom pada matriks A harus sama dengan banyaknya baris pada matriks B. Jika hal ini tidak dipenuhi menjadikan hasil kali matriks tidak didefinisikan.

Baca juga: Materi dan Contoh Soal Matriks Pangkat

Pages: 1 2 3 4