Materi Rumus Matriks Matematika SMA

Penemu matriks adalah Arthur Cayley yang menerbitkan definisi abstrak matriks pada tahun 1958. Cayley menerapkan matriks pada sistem persamaan linier dengan menyatakan ilmu matriks akan cukup penting dikembangkan pada berbagai hukum aritmatika. Misalnya, dalam sistem aljabar hingga pengaplikasian dalam grafik komputer.

Untuk yang pertama kali melihat penyusunan matriks pasti akan terlihat bingung dengan penyusunan angka-angkanya. Pada matriks sendiri memiliki model matematika yang berbeda dengan persoalan-persoalan matematika lainnya. Berikut contoh penyusunan sebuah matriks.

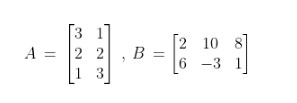
Model matematika di atas dinamakan matriks yang dibentuk persegi atau persegi panjang. Angka-angka dalam matriks disusun atas baris dan kolom dan ditulis dalam sebuah kurung berbentuk kotak. Dari model matriks di atas dapat kita ketahui bahwa matriks A memiliki 3 baris dan 2 kolom, sedangkan matriks B memiliki 2 baris dan 3 kolom. Agar lebih jelas menelaah baris dan kolomnya mari kita lihat gambar berikut.

Baca juga: Pengertian Transpose Matriks Dan Contoh Soal

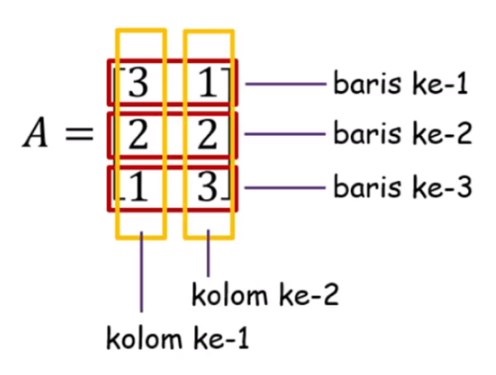
Keterangan: Baris adalah susunan horizontal dari kanan – kiri, sedangkan kolom adalah susunan vertikal dari atas – bawah.