Menghitung Luas Dan Keliling Segitiga

Rumus Segitiga – Sebagian besar dari Anda mungkin sudah paham tentang rumus rumus bangun datar segitiga. Hal ini karena pada saat duduk di bangku Sekolah Menengah Pertama sudah pasti mempelajari segitiga. Nah, disini kami akan mengajak Anda untuk mempelajari mengenai segitiga lebih mendalam.

Pada kesempatan kali ini kami akan menjelaskan mengenai cara bagaimana cara menghitung luas dan keliling segitiga. Namun sebelum itu kami akan mengulas terlebih dahulu mengenai pengertian, karakteristik dan jenis-jenis bangun datar segitiga. Untuk lebih jelasnya mari langsung saja simak ulasan selengkapnya.

Pengertian Segitiga

Pengertian segitiga merupakan sebuah bangun datar yang mempunyai 3 buah sisi, dimana masing-masing sisi tersebut bertemu pada 3 buah titik sudut.

Segitiga bisa dibilang merupakan sebuah datar paling sederhana karena bangun datar yang satu ini merupakan unsur pembentuk bangun datar yang lainnya seperti lingkaran, persegi, persegi panjang, dan juga unsur bangun datar pembentuk bangun ruang seperti limas dan prisma.

Pada umumnya jumlah keseluruhan sudut yang dimiliki oleh bangun datar segitiga 180 derajat. Maka dari itu, kita bisa melakukan perhitungan pada salah satu bangun datar segitiga tersebut jika sudut-sudut lainnya yang dapat diketahui.

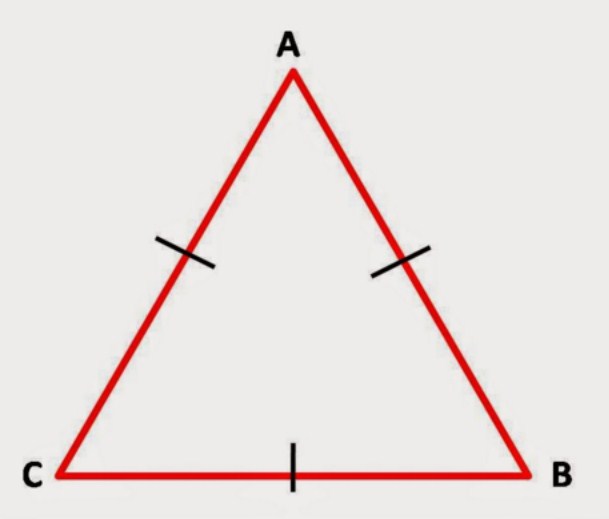
Silahkan Anda perhatikan gambar bangun datar segitiga dibawah ini:

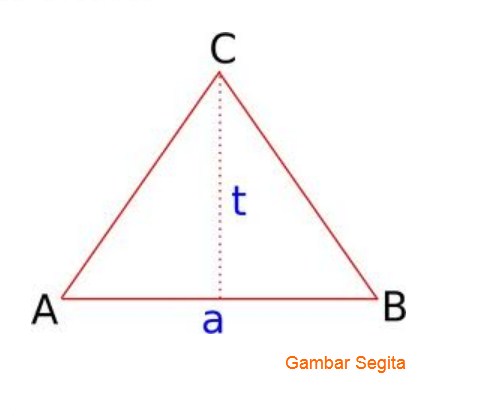
Dari gambar bangun datar tersebut, keterangannya adalah sebagai berikut:

AB, BC dan CA merupakan sisi-sisi keliling

A = alas

T = tinggi

Baca Juga: Rumus Luas Dan Keliling Bangun Datar

Jenis-Jenis Bangun Datar Segitiga

Segitiga memiliki jenis yang sangat beragam berdasarkan panjang sisi dan juga sudut yang telah membentuk segitiga tersebut. Adapun jenis-jenis bangun datar segitiga adalah sebagai berikut ini:

Jenis-Jenis Segitiga Berdasarkan Panjang Sisi

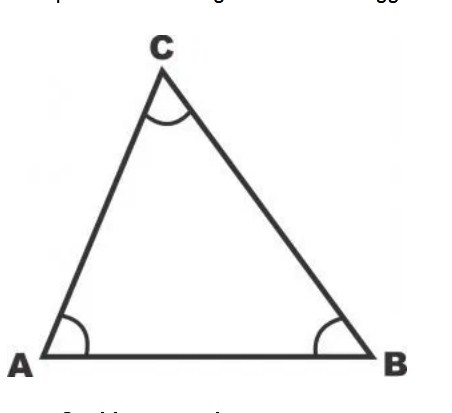
• Segitiga Sama Sisi

Segitiga sama sisi adalah sebuah bangun datar yang memiliki sisi sama panjang. Disamping itu, ketiga sudut yang telah dibentuk oleh segitiga sisi memiliki besar yang sama, yakni 60 derajat, karena jumlah sudut yang dimiliki oleh bangun datar segitiga adalah 180 derajat.

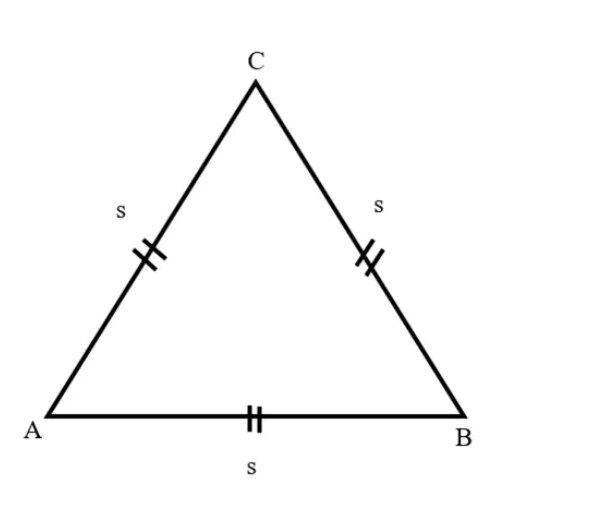
Untuk memudahkan pemahaman Anda mengenai segitiga sama sisi, mari simak penjelasan selengkapnya mengenai sifat-sifat segitiga sama sisi di bawah ini:

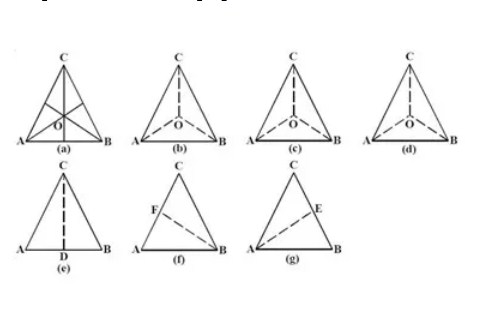
Dari gambar (b) – (d) bisa dilihat bahwa segitiga ABC dapat menempati bingkainya yang dimana menggunakan 3 cara yaitu, diputar hingga 120 derajat yang titik pusatnya adalah O (bisa Anda lihat arah putaran) pada (gambar b) diputar hingga sejauh 240 derajat yang berpusat di titik O (pada gambar c) yang diputar hingga sejauh 360 derajat (hingga satu putaran penuh) yang berpusat pada titik O (pada gambar d).

Dilihat dari gambar a sampai f, maka segitiga ABC sama sisi mempunyai simetri putar hingga tingkat 3. Sedangkan gambar e, f dan g yang caranya membalik dapat menempati bingkai secara tepat. Dalam hal ini, bangun segitiga ABC mempunyai 3 sumbu simetri.

Sementara jika dilihat secara menyeluruh pada gambar diatas, maka berarti sumbu simetrinya adalah CD, BF dan AE. Dengan demikian segitiga sama sisi dapat menempati bingkainya dengan tepat hingga 6 cara.

Jadi dapat disimpulkan bahwa beberapa sifat yang dimiliki oleh segitiga sama sisi yaitu mempunyai simetri putar hingga sebanyak 3 tingkat, 3 buah sumbu simetri, 3 sisi yang sama panjang, 3 sudut sama besar yaitu 60 derajat, dan dapat menempati bingkainya sampai dengan 6 cara.

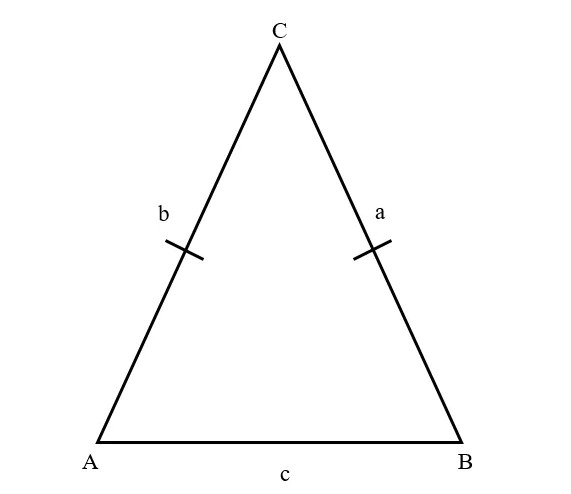
• Segitiga Sama Kaki

Segitiga sama kaki merupakan bangun datar segitiga yang dimana kedua sisinya memiliki ukuran sama panjang. Jenis segitiga yang satu ini mempunyai dua buah sudut dengan ukuran sama besar, yakni sudut yang saling berhadapan.

Berikut ini adalah sifat-sifat yang dimiliki oleh segitiga sama kaki:

• Jika diputar hingga satu putaran penuh maka bangun datar segitiga sama kaki dapat menempati bingkainya secara tepat pada satu cara. Sehingga bangun datar segitiga sama kaki ini hanya mempunyai satu simetri putar.
• Segitiga sama kaki juga hanya mempunyai satu sumbu simetri saja.

• Segitiga Sembarang

Segitiga sembarang adalah jenis segitiga yang dimana ketiga sisinya tidak memiliki ukuran sama panjang dan untuk ketiga sudutnya juga tidak sama besar.

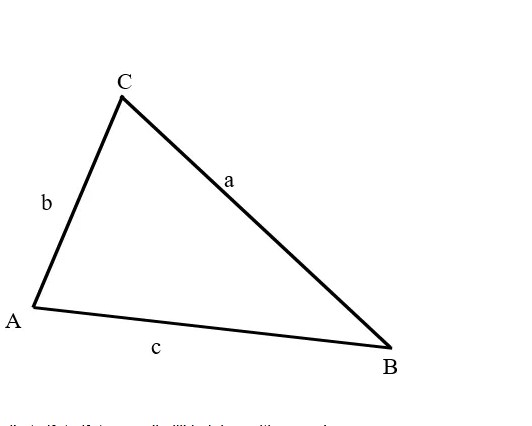
Adapun sifat-sifat yang dimiliki oleh segitiga sembarang adalah sebagai berikut:

• Memiliki tiga buah sisi yang memiliki ukuran tidak sama panjang. Silahkan Anda perhatikan gambar segitiga sembarang diatas, ketiga sisi yang kami maksud yaitu Panjang BA ≠ CB ≠ AC.
• Tidak mempunyai simetri lipat.
• Hanya memiliki satu buah simetri putar.
• Ketiga sudutnya memiliki ukuran besar yang berbeda.

Jenis Segitiga Berdasarkan Besar Sudut

• Segitiga Lancip

Segitiga lancip adalah sebuah segitiga yang dimana ketiga buah sudutnya membentuk sudut lancip.  Sudut lancip sendiri merupakan sebuah sudut yang memiliki kisaran mulai dari 0 sampai dengan 90 derajat.

• Segitiga Tumpul

Segitiga tumpul adalah sebuah segita yang dimana salah satu sudutnya membentuk sudut tumpul. Sudut tumpul merupakan sudut yang dimana besarnya di kisaran 90 sampai dengan 180 derajat.

• Segitiga Siku-siku

Segitiga siku-siku merupakan sebuah segitiga yang dimana salah satu sudutnya membentuk sudut hingga 90 derajat.

Rumus Rumus Untuk Menghitung Segitiga