Rumus Integral Tertentu dan Tak Tentu

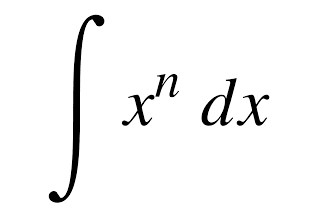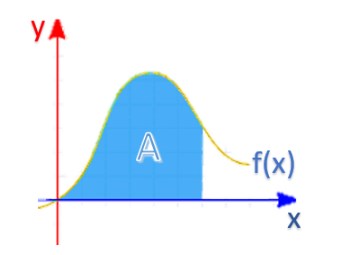
Selain berdasarkan sebuah grafik, integral tak tentu dapat diperlihatkan dengan sifat-sifat yang melatar belakanginya sebagai berikut.

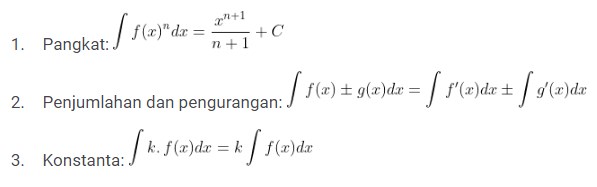
Baca juga: Rumus Turunan Fungsi Trigonometri

Rumus Integral Tentu

Konsep dari integral tentu berhubungan dengan sifat dari definite integral dan memerlukan rumus yang dapat digunakan untuk menyelesaikan suatu permasalahan pada integral sebagai berikut.

Integral dari f(x) terhadap dx dari b sampai a adalah F(a) dikurangi F(b). F'(x) adalah fungsi yang turunannya bernilai f(x) yang merupakan hasil dari definite integral adalah suatu angka yang pasti.

Baca juga: Materi Limit Fungsi Trigonometri

Rumus Integral Tak Tentu

Dalam integral tak tentu terdapat nilai atau batasannya yang belum pasti sehingga terdapat nilai konstanta di dalamnya. Dengan begitu, penyusunan rumus integral tak tentu dapat ditunjukkan sebagai berikut.

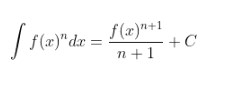
Contoh Soal

Setelah mempelajari materi mengenai integral tentu dan tak tentu tentunya kalian butuh beberapa penerapannya pada sebuah soal. Agar dapat memahami lebih dalam lagi, berikut beberapa contoh soal beserta pembahasan mengenai materi integral tentu dan tak tentu.

1. Tentukan hasil integral

Pembahasan:

Lakukan pengubahan bentuk akar menjadi f(x)n dan sesuaikan dengan rumus integral tak tentu.

2. Tentukan hasil integral berikut