Pembahasan Rumus Diferensial (Turunan)

Pembahasan Rumus Diferensial (Turunan) – Dalam ilmu matematika, kita akan menemukan beragam rumus yang dapat menjelaskan sebuah fungsi. Salah satunya pada fungsi turunan atau yang biasa disebut diferensial.

Fungsi diferensial menjelaskan suatu persamaan dengan pelibatan satu atau beberapa turunan fungsi yang belum diketahui sebelumnya. Biasanya, turunan atau diferensial akan digunakan sebagai alat untuk menyelesaikan beragam masalah.

Fungsi F yang akan dijadikan fungsi turunan akan menjadi bentuk F’. Dalam pembentukannya akan memiliki nilai yang tidak beraturan. Turunan fungsi yang belum diketahui dan tidak beraturan mungkin dapat juga melibatkan fungsi itu sendiri dan beberapa konstanta.

Baca juga: Rumus Turunan Fungsi Trigonometri

Pada pembahasan kali ini, kalian akan mempelajari mengenai diferensial atau turunan dengan beberapa rumusnya. Berikut pembahasannya.

Konsep Turunan

Konsep turunan awalnya digunakan pada ilmu kalkulus. Saat itu, Isaac Newton yang merupakan seorang matematikawan dan fisikawan Inggris bersama Gottfried Wilhelm Leibniz matematikawan Jerman memahami teori ini.

Teori diferensial diciptakan berdasarkan jenis teorinya yang membahas perubahan pada variabel terikat. Hal ini diakibatkan adanya perubahan juga dari variabel bebasnya. Perubahan pada variabel bebas ini tergolong ke dalam perubahan yang sangat keci.

Misalnya, Y adalah fungsi dari X atau Y = F (x) mendapatkan turunan dari Y terhadap X.

Baca juga: Faktor yang Mempengaruhi Tumbuh Kembang Manusia

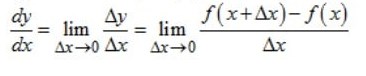
Rumus Turunan

Rumus turunan memiliki berbagai macam jenisnya. Untuk itu, perhatikan beberapa jenis rumusnya berikut ini.

Rumus 1

Jika y = c x n dengan c dan n konstanta real menjadikan dy/dx = cn x n-1

contoh

y = 2 × 4 maka dy/dx = 4.2 × 4-1 = 8 × 3

Rumus 2

Jika y = f(x) + g(x), turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)

contoh

y = x3 + 2 × 2 maka y’ = 3 × 2 + 4x

y = 2 × 5 + 6 maka y’ = 10×  4 + 0 = 10 × 4

Rumus 3

Jika y = c dengan c adalah konstanta menjadikan dy/dx = 0

contoh

jika y = 6, turunannya sama dengan nol

Baca juga: Pengurangan dan Penjumlahan Vektor Beserta Contoh Soal

Rumus 4

Jika y f(x).g(x) menjadikan y’ = f'(x) . g(x) + g'(x) . f(x)

contoh

y = x2 (x2 + 2) maka

f(x) = x2

f'(x) = 2x

g(x) = x2+2

g'(x) = 2x