Jika Tautan Rusak atau Halaman Error,

Hubungi Halaman "Kontak Admin"

×

Materi, Rumus Gerak Parabola dan Contoh Soal

August 2nd, 2022 By

x = V_{x0} \times t \newline \newline V_{x0} = \frac{x}{t} = \frac{90 m}{3.19 s} = 28,21 \: m/s

Jadi, kecepatan yang harus dicapai harus sebesar 28,21 m/s atau sekitar 100 km/h (101,55 km/h).



Soal 2

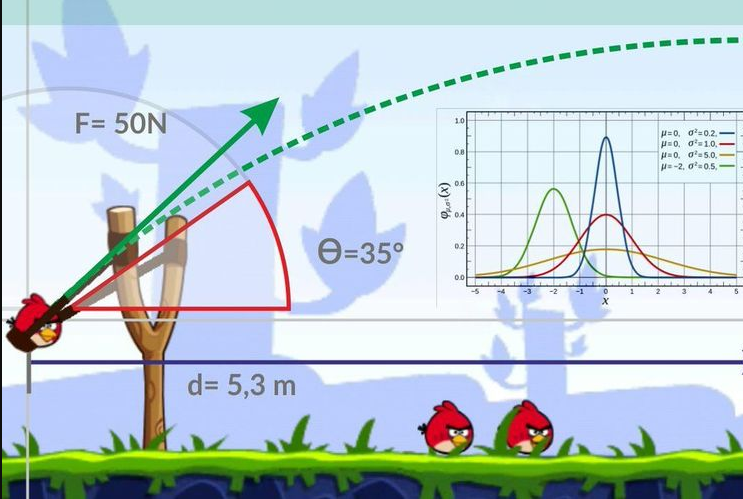
Sebuah bola ditendang membentuk sudut (\theta_0 = 37^{\circ}) dengan kecepatan . Hitunglah (a) ketinggian maksimum bola, (b) waktu tempuh bola hingga bola mendarat di tanah (c) seberapa jauh bola mencapai tanah, (d) kecepatan bola di ketinggian maksimum, dan (e) percepatan saat ketinggian maksimum. Abaikan gesekan udara dan rotasi pada bola.

Pembahasan:

Gambarlah lebih dahulu lintasan gerak parabola objek tersebut. Perhatikan gambar dibawah ini dengan lebih teliti.

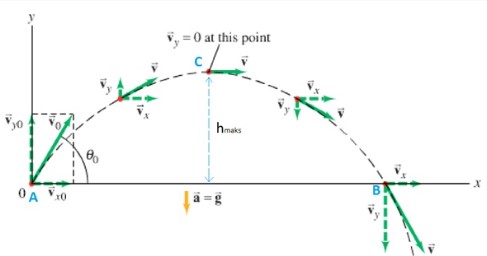
Cari kedua komponen kecepatannya untuk mengisi variabel yang diperlukan:

V_{x0} = V_0 \cos 37^{\circ} = 20 m/s \times 0,799 = 16 m/s \newline \newline V_{y0} = V_0 \sin 37^{\circ} = 20 m/s \times 0,602 = 12 m/s.

(a) Dengan menggunakan rumus kecepatan komponen vertikal, kita bisa mendapatkan selang waktu tempuh saat bola mencapai titik tertinggi.

V_y = V_{y0} - gt \newline \newline 0 = V_{y0} - gt \newline \newline V_{y0} = gt \newline \newline t = \frac{V_{y0}}{g} = \frac{12 m/s}{9,8 m/s^2} = 1,22 s

Kemudian, gunakan rumus untuk mencari ketinggian benda:

y = V_{y0} t - \frac{1}{2} gt^2 \newline \newline y = 12 m/s \cdot 1,22 s - \frac{1}{2} \cdot 9,8 m/s^2 \cdot (1,22 s)^2 \newline \newline y = 7.35 m.

(b) dan (c):

Pertama, kita pakai rumus untuk mencari jarak tempuh maksimum:

x_{max} = (V_0^2 \sin 2 \theta_0)/g \newline \newline x_{max} = ((20 \: m/s)^2 \sin 2(37^{\circ}))/(9,8 m/s^2 \newline \newline x_{max} = 39,2 m.

Kemudian, kita dapat mencari jarak tempuh bola maksimum:

x_{max} = V_{max} \times t_{max} \newline \newline t_{max} = \frac{x_{max}}{V_x} = \frac{39,2 \: m}{16 \: m/s} = 2,45 s.

(d) Di titik tertinggi, tidak terdapat komponen kecepatan vertikal. Jadi kecepatan bola saat di titik tertinggi adalah:

V_{max} = V_{x0} = V_0 \cos 37^{\circ} = 16 m/s.

(e) Besarnya percepatan sama di setiap lintasan, yakni sebesar 9,8 \: m/s^2 ke bawah.



Pages: 1 2 3 4

RELATED POST