Rumus Menghitung Relasi Dan Fungsi

Rumus Menghitung Relasi Dan Fungsi – Saat belajar matematika maka kita akan menjumpai materi relasi dan fungsi. Keduanya ini biasanya diajarkan di tingkat sekolah menengah pertama atau kelas 8. Untuk memahami apa itu relasi dan fungsi beserta rumus hingga cara menghitungnya, pada kesempatan ini kita bahas tentang materi tersebut lebih dalam. Kita awali dari definisi relasi.

Apa itu Relasi?

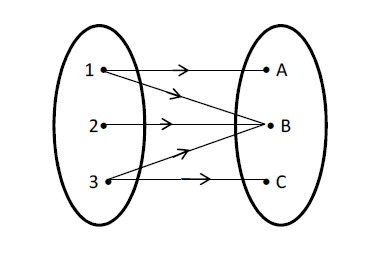
Dalam kamus bahasa Indonesia relasi diartikan sebagai hubungan dan bisa dibilang merupakan turunan dari bahasa Inggris, relation. Dalam konteks himpunan, relasi adalah hubungan antara anggota himpunan dengan anggota himpunan lainnya. Lebih jelasnya, kita bayangkan ada dua himpunan yang diberi nama Himpunan A dan Himpunan B. Keduanya disebut mempunyai relasi apabila ada anggota himpunan satu yang berpasangan dengan anggota himpunan lainnya.

Baca juga: Rumus Korespondensi Satu-Satu

Jenis Relasi

Relasi terbagi menjadi beberapa macam. Antara lain relasi invers, simetrik, refleksif, anti simetrik, hingga relasi transitif. Berikut penjelasan singkat masing-masing jenis tersebut:

Relasi Refleksif

Suatu relasi R dalam A disebut mempunyai sifat refleksif apabila setiap elemen A berhubungan dengan dirinya. Sebagai gambaran, relasi yang mempunyai sifat refleksif merupakan relasi “x selalu bersama y”. Artinya apabila x dan y merupakan anggota himpunan seluruh manusia, maka dapat dikatakan bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.

Relasi Irefleksif

Selanjutnya juga ada relasi irefleksif. Relasi R dalam A dikatakan irefleksif apabila setiap elemen A tidak berkaitan dengan dirinya sendiri. Contohnya relasi refleksif merupakan relasi “x dapat menambal gigi y dengan sempurna”, dengan pernyataan x dan y merupakan dokter gigi. Apabila setiap orang hanya bisa menambal gigi orang lain dengan sempurna, maka hal tersebut termasuk ke dalam sifat irefleksif. Sebab tidak ada dokter gigi yang bisa menambal giginya sendiri.

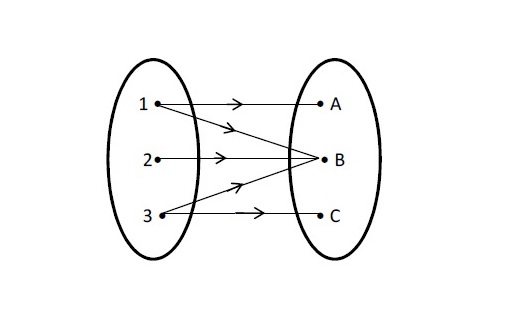
Relasi Simetrik

Suatu relasi dikatakan mempunyai sifat simetrik apabila setiap pasangan anggota berhubungan satu sama lain. Artinya jika a terhubung dengan b, maka b secara otomatis juga terhubung dengan a. Dengan kata lain ada hubungan timbal balik dari penjelasan tersebut.

Misanya relasi genap tergolong relasi simetrik. Sebab untuk sembarang x dan y yang dipilih, apabila memenuhi relasi tersebut maka kita bisa menukarkan nilai x dan y, dan membuat relasi tersebut bisa terpenuhi.

Relasi Anti-simetrik

Relasi anti-simetrik adalah sebuah hubungan dimana setiap a dan b yang terhubung hanya ada satu saja terhubung. Dengan catatan a dan b berlainan. Contohnya jika  R dari suatu relasi pada himpunan bilangan asli didefinisikan y habis dibagi x, maka R merupakan relasi anti-simetrik. Karena apabila b habis dibagi a, dan aa habis dibagi b, maka dapat disimpulkan bahwa a = b.

Relasi Transitif

Sebuah relasi dikatakan transitif apabila mempunyai sifat jika a berhubungan dengan b, dan b berhubungan dengan c, maka a berhubungan secara langsung dengan c.Kita ambil contoh relasi dua transitif. Misalnya pada bilangan 5, 6, dan 7 berlaku 5 < 6, 6 < 7, dan 5 < 7.

Baca juga: Fungsi Komposisi Dan Fungsi Invers

Menyatakan Relasi

Menyatakan relasi antara dua himpunan bisa dilakukan dalam tiga cara. Antara lain dengan diagram panah, himpunan pasangan berurutan, dan diagram kartesius. Berikut penjelasan singkat ketiganya:

Diagram Panah

Diagram panah adalah cara termudah yang bisa kita lakukan untuk menyatakan sebuah relasi. Selain itu bentuk diagram ini juga yang paling sering dijumpai dalam soal yang berkaitan dengan relasi. Diagram panah membentuk pola dari suatu relasi ke bentuk gambar arah panah yang menyatakan hubungan anggota himpunan satu dengan anggota himpunan lainnya.

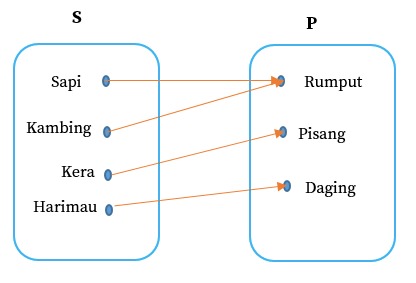
Ciri-ciri dari diagram ini terletak pada bentuknya yang memiliki dua kolom terpisah dan masing-masing kolom memuat himpunan yang bersesuaian. Kedua kolom tersebut dihubungkan dengan sebuah anak panah.

Himpunan Pasangan Berurutan

Tidak hanya diagram panah saja, relasi juga bisa dinyatakan dengan memakai himpunan pasangan berurutan. Lalu bagaimana cara membuatnya? Cukup dengan memasangkan himpunan satu dengan himpunan kedua secara berurutan. Simak contoh berikut ini.

A = {Sapi, Kambing, Kera, Harimau}

B = {Rumput, Pisang, Daging}

C = {(Sapi, Rumput), (Kambing, Rumput), (Kera, Pisang), (Harimau, Daging)}

Dari contoh di atas antara himpunan A dan himpunan B merupakan himpunan pasangan berurutan atau juga bisa dilammbangkan (x, y) dengan x ∈ A dan y ∈ B.

Diagram Cartesius

Diagram cartesius merupakan sebuah cara yang dilakukan untuk menyatakan relasi antara dua himpunan dari pasangan berurutan, lalu ditulis kembali dalam bentuk titik-titik. Diagram ini mempunyai dua sumbu, yakni sumbu x dan sumbu y. Untuk membuat diagram ini masing-masing anggota himpunan diletakkan di titik yang bersesuaian. Dengan ketentuan himpunan A berada di sumbu x dan himpunan B berada di sumbu y. Contohnya seperti gambar di bawah ini.

Baca juga: Cara Mencari KPK Dan FPB

Apa itu Fungsi?

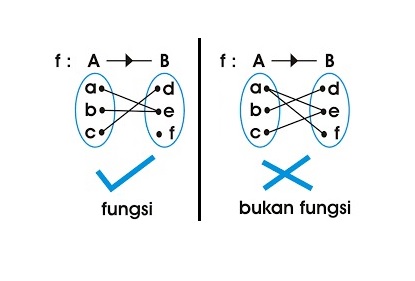
Setelah membahas relasi, kini kita bahas apa itu fungsi. Fungsi atau pemetaan adalah relasi dari himpunan A ke himpunan B, apabila setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B. Untuk dicatat, seluruh anggota himpunan A atau daerah asal disebut dengan istilah domain. Sementara seluruh anggota himpunan B atau daerah kawan disebut kodomain.

Sementara hasil pemetaan antara domain dan kodomain disebut range fungsi atau juga bisa dinamai daerah hasil. Cara menyatakan fungsi ini tidak jauh berbeda dari relasi. Kita bisa menyatakannya dalam bentuk diagram panah, diagram cartesius, hingga himpunan pasangan berurutan.

Contohnya ada dua himpunan sebagai berikut:

B = {Garam, Gula, Lada, Cuka, Pare}

C = {Asin, Manis, Pedas, Asam, Pahit}

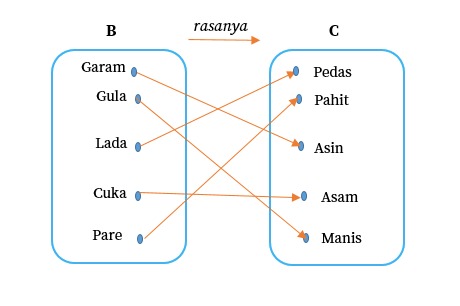
Dari contoh di atas kita tahu bahwa setiap anggota himpunan B berpasangan dengan satu anggota himpunan C. Kesimpulannya setiap fungsi adalah relasi. Akan tetapi tidak semua fungsi menunjukkan relasi. Fungsi merupakan bentuk relasi yang memenuhi syarat khusus, yakni setiap anggota himpunan asal mempunyai satu pasang anggota himpunan hasil.

Cara Menghitung Nilai Fungsi

Kita lihat contoh diagram panah di bawah ini.

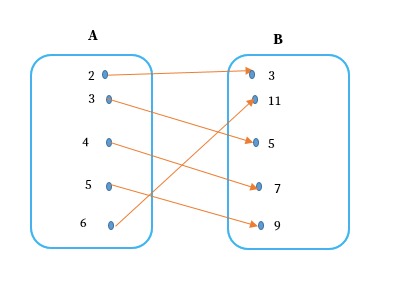
• Untuk sembarang anggota A, misalnya 2, daerah hasil yang ditunjuk adalah 3.
• Untuk sembarang anggota A, misalnya 3, daerah hasil yang ditunjuk adalah 5 dan seterusnya.

Kira-kira, apa hubungan antara himpunan A dan B?

Himpunan B merupakan 2 × anggota himpunan A – 1. Secara matematis, dinyatakan sebagai berikut.

x -> 2x – 1

Jika relasi 2x – 1 dinotasikan sebagai f, maka f memetakan x ke (2x – 1). Secara matematis, ditulis sebagai berikut.

f: x -> (2x – 1)

Rumusan f(x) = 2x – 1 nantinya kita kenal sebagai rumus fungsi.

Baca juga: Rumus Barisan Dan Deret Aritmatika

Jenis Fungsi

Sama seperti relas, fungsi juga mempunyai beberapa jenis yang harus kita ketahui. Antara lain fungsi konstan, fungsi identitas, fungsi linear, fungsi kuadrat, fungsi tangga, fungsi modulus, serta fungsi ganjil dan genap. Berikut penjelasan singkatnya:

1. Fungsi Konstan. Merupakan sebuah fungsi f : A?B yang ditentukan dengan memakai rumus f(x). Jika setiap anggota domain fungsi selalu berlaku  f(x) = C, dimana C merupakan bilangan konstan.
2. Fungsi Identitas. Adalah sebuah fungsi f yang dinyatakan dengan rumus f(x) = x. Fungsi ini juga sering dinyatakan dalam lambang I sehingga I(x) = x.
3. Fungsi Modulus. Fungsi modulus juga bisa disebut dengan fungsi harga mutlak. Fungsi ini merupakan fungsi f yang memiliki bentuk nilai yang mutlak.
4. Fungsi Linear. Fungsi linear adalah suatu fungsi f(x) yang jika fungsi itu ditentukan oleh f(x) = ax + b, di mana a ? 0, a dan b merupakan bilangan konstan dan mempunyai grafik berupa garis lurus.
5. Fungsi Kuadrat. Fungsi kuadrat adalah sebuah fungsi f(x) yang ditentukan oleh f(x) = ax2 + bx + c, di mana a ? 0 dan a, b, dan c merupakan bilangan konstan dan memiliki grafik berupa parabola.
6. Fungsi Tangga. Fungsi tangga juga biasa disebut fungsi bertingkat. Fungsi tangga merupakan sebuah fungsi f(x) yang grafik fungsi f(x) mempunyai bentuk interval-interval yang sejajar.
7. Fungsi Modulus. Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.
8. Fungsi Ganjil dan Fungsi Genap. Suatu fungsi f(x) disebut fungsi ganjil apabila berlaku f(–x) = –f(x) dan disebut fungsi genap apabila berlaku f(–x) = f(x). Jika f(–x) ? –f(x) maka fungsi ini tidak genap dan tidak ganjil.

Fungsi Invers

Perlu dicatat bahwa seluruh himpunan yang dipetakan oleh fungsi pasti memiliki invers. Sementara invers dari himpunan tersebut bisa berupa fungsi maupun bukan fungsi. Fungsi f akan memiliki invers, yakni f-1 apabila fungsi f bijektif atau termasuk dalam korespondensi satu-satu.

Jika ingin menentukan invers dari fungsi maka kita bisa melakukan beberapa cara, yaitu:

1. Membuat permisalan f(x) = y pada persamaan
2. Persamaan tersebut disesuaikan dengan f(x) = y, sehingga dapat ditemukan fungsi dalam y dan dinyatakan x = f(y).
3. Selanjutnya gani y dengan x, sehingga f(y) = f –1(x).

Perbedaan Relasi dan Fungsi

Dari penjelasan di atas, mungkin kalian belum begitu paham apa perbedaan antara relasi dan fungsi. Sederhananya, relasi merupakan hubungan antara daerah asal (domain) dengan daerah kawan (kodomain). Sementara fungsi adalah relasi yang memasangkan tiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawan.

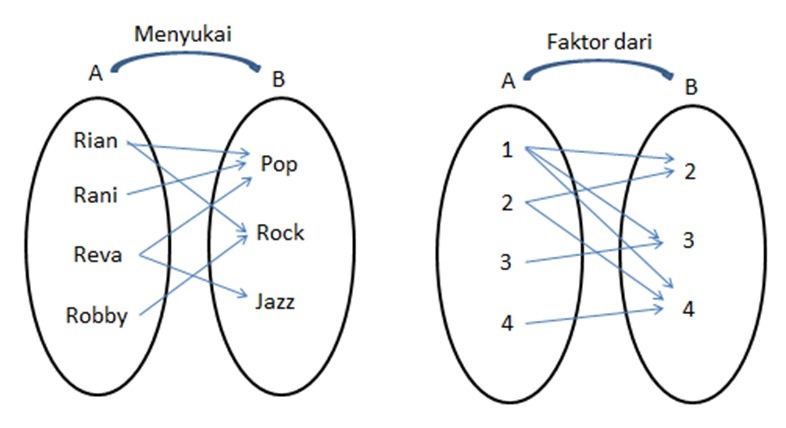
Di samping itu cara memasangkan anggota himpunan ke daerah asal, baik relasi maupun fungsi juga berbeda. Pada relasi tidak terdapat aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi itu sendiri. Masing-masing anggota himpunan daerah asal bisa memiliki pasangan lebih dari satu atau boleh tidak memiliki pasangan.

Sementara pada fungsi masing-masing anggota himpunan daerah asal dipasangkan dengan syarat tertentu. Setiap anggota himpunan daerah asal memiliki pasangan dan hanya boleh dipasangkan dengan satu anggota himpunan daerah kawan.

Baca juga: Belajar Rumus Excel Yang Sering Digunakan

Contoh Soal

Soal 1

Diketahui fungsi f : x → 3x + 3 pada himpunan bilangan bulat. Tentukan:

1. f(3)
2. bayangan (-2) oleh f
3. nilai f untuk x = -4
4. nilai x untuk f(x) = 6
5. nilai a jika f(a) = 12

Fungsi f : x → 3x + 3

Rumus fungsi: f(x) = 3x+3

f(3) = 3(3)+3 = 12

bayangan (-2) oleh f sama dengan f (-2), jadi f(-2) = 3(-2)+3 = -3

nilai f untuk x = -4 adalah f (-4) = 3(-4)+3 = -9

nilai x untuk f(x) = 6 adalah