Pertidaksamaan Logaritma dan Contoh Soal

Dengan begitu, penyelesaiannya dapat menjadi 0 < x < 1 : √10 atau x > 10.

Selain beberapa sifat pertidaksamaan di atas, operasi logaritma dapat diselesaikan dengan sebuah harga yang mutlak. Pertidaksamaan logaritma dengan harga mutlak biasanya penyelesaiannya mengikuti sifat-sifat harga mutlak dan sifat logaritma sendiri. Berikut sifat dari harga mutlak sendiri.

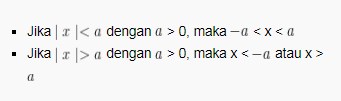
Misalnya, kita dapat mengerjakan penyelesaian pertidaksamaan logaritma harga mutlak pada contoh soal berikut |³log (x + 1)| < 2.

Baca juga: Contoh Soal Peluruhan Matematika SMA Kelas 10

Contoh Soal

Setelah mempelajari beberapa pembahasan di atas mengenai pertidaksamaan logaritma di atas, alangkah baiknya kalian dapat menerapkannya lebih lanjut dengan mempelajari beberapa contoh soal berikut dengan pembahasannya.

1. Tentukan hasil dari pertidaksamaan logaritma 2 log(x + 1) ≤ log (x + 4) + log 4.

Pembahasan:

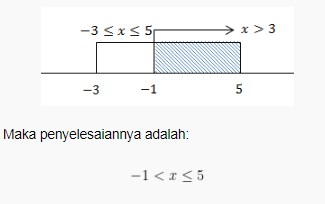
Dengan syarat (x + 1)²  > 0 atau x < -1 dengan x < -1. Garis bilangannya dapat digambar sebagai berikut.

2. Nilai xyang memenuhi pertidaksamaan ²log(2x−3)<3 adalah ….